Concetti Chiave
- L'energia potenziale del sistema è calcolata sommando le energie potenziali di tutte le coppie di cariche.
- Il calcolo dell'energia potenziale tra due cariche si effettua con la formula U = k0 * (Q1Q2)/r.
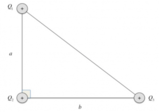
- Le distanze tra le cariche sui lati del quadrato sono 4,8 cm, mentre per le diagonali si utilizza 6,79 cm.
- I valori delle energie potenziali calcolate per ciascuna coppia di cariche sono sommati per ottenere l'energia totale del sistema.
- L'energia potenziale totale del sistema di cariche è 2,5 * 10-6 J.
In questo appunto vedremo la soluzione di un esercizio, la cui richiesta è il calcolo dell'energia potenziale di un sistema di 4 cariche puntiformi, poste ai vertici di un quadrato. Vediamo il testo dell'esercizio.
Testo dell'esercizio
Quattro cariche puntiformi di valori rispettivamente
,
,
,
, occupano nel vuoto i vertici di un quadrato di lato
.
Determina l'energia potenziale del sistema.
Svolgimento dell'esercizio
Nel caso di cariche puntiformi, l'energia potenziale del sistema è data dalla somma delle energie potenziali che si ottengono scegliendo le cariche a coppie in tutti i modi possibili. Dunque andremo a calcolare
energie potenziali possibili
.
Calcoliamo quindi ognuna di esse utilizzando la formula dell'energia potenziale
,
trasformando prima le grandezze nelle giuste unità di misura.
Cominciamo dalle cariche
e
:
Passiamo alle cariche
e
:
Per le cariche
e
si ha:
Infine, per le cariche
e
si ha:
Nel caso delle altre due coppie, dobbiamo considerare come distanza la diagonale del quadrato, che si ottiene moltiplicando il lato per
:
Calcoliamo quindi l'energia potenziale per le cariche
e
:
E per le cariche
e
:
Sommiamo ora le sei energie potenziali per trovare quella del sistema:
Domande da interrogazione
- Come si calcola l'energia potenziale di un sistema di cariche puntiformi?
- Qual è la distanza utilizzata per calcolare l'energia potenziale tra le cariche sui vertici opposti del quadrato?
- Quali sono i valori delle energie potenziali calcolate per ciascuna coppia di cariche?
- Qual è l'energia potenziale totale del sistema di cariche?
L'energia potenziale di un sistema di cariche puntiformi si calcola sommando le energie potenziali di tutte le coppie di cariche possibili, utilizzando la formula [math] U = k_0 \cdot \frac{Q_1 Q_2}{r} [/math].
La distanza utilizzata per le cariche sui vertici opposti del quadrato è la diagonale, calcolata come [math] d = l \sqrt2 [/math], dove [math] l [/math] è il lato del quadrato.
Le energie potenziali calcolate sono: [math] U_{(1,2)} = -18,73 \cdot 10^{-7} J [/math], [math] U_{(1,4)} = 29,97 \cdot 10^{-7} J [/math], [math] U_{(2,3)} = -15,45 \cdot 10^{-7} J [/math], [math] U_{(3,4)} = 24,72 \cdot 10^{-7} J [/math], [math] U_{(2,4)} = -13,24 \cdot 10^{-7} J [/math], [math] U_{(1,3)} = 17,28 \cdot 10^{-7} J [/math].
L'energia potenziale totale del sistema di cariche è [math] U_{TOT} = 2,5 \cdot 10^{-6} J [/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
