Concetti Chiave
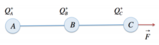
- Tre fili infiniti, disposti su tre vertici di un quadrato, hanno correnti i con orientamenti differenti: il filo 1 segue l'asse z, mentre i fili 2 e 3 sono opposti.
- Nel quarto vertice del quadrato si trova un circuito con momento di dipolo magnetico parallelo al campo magnetico nel punto P.
- Il campo magnetico in P è determinato solo dal filo 2 e si calcola come B = (mu_o)/(2π) * i/D, con D = d√2.
- L'energia potenziale del dipolo in campo magnetico è U = -muB, e la corrente i si esprime come i = -(U * 2πD)/(mu_omu).
- La forza per unità di lunghezza tra i fili 1 e 3 è F = (mu_o)/(2π) * (i^2)/D, calcolata in funzione di valori noti.
Tre fili infiniti paralleli all'asse z, sono posti su tre vertici di un quadrato di lato
[math]d[/math]
e percorsi dalla corrente i dello stesso valore: il verso della corrente del filo 1 è parallelo al versore [math]u(z)[/math]
dell'asse z, quello nei fili 2 e 3 è opposto. Nel punto P, quarto vertice del quadrato, è posto un piccolo circuito di momento di dipolo magnetico di modulo [math]\mu[/math]
parallelo al campo magnetico [math]B(p)[/math]
in quel punto. L'energia potenziale del dipolo risulta [math]U(p)[/math]
. Calcolare: a) il valore del campo magnetico B in P b) il valore della corrente i che percorre i tre fili c) il modulo della forza per unità di lunghezza F(13) tra i fili 1 e 3
Dato che i campi prodotti in P dai fili 1 e 3 si elidono resta solo quello prodotto dal filo 2:
[math]B=(\mu_o)/(2\pi) \cdot i/D[/math]
dove [math]D=d\sqrt2[/math]
da cui ricavo [math]i=(B \cdot 2\pi D)/(\mu_o)[/math]
Ora l'energia potenziale U di un dipolo posto in un campo magnetico è: [math]U=-\mu B \cos \theta=-\mu B[/math]
( [math]\mu[/math]
=modulo momento di dipolo, [math]\theta[/math]
= angolo tra [math]\vec{B}[/math]
e [math]\vec{\mu}v[/math]
)
Quindi [math]B=-U/(\mu)[/math]
ed i diventa: [math]i=-(U*2 \pi D)/(\mu_o\mu)[/math]
La forza ( per unità di lunghezza ) tra i fili 1 e 3 è data dalla formula [math]F=(\mu_0)/(2\pi)*(i_1i_3)/D=(\mu_o)/(2\pi)*(i^2)/D[/math]
Riassumendo abbiamo:
[math]B=-U/(\mu),i=-(U*2\pi D)/(\mu_o\mu),F=(\mu_o)/(2\pi)*(i^2)/D[/math]
ovvero i dati richiesti in funzione di dati tutti noti.
FINE
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
