Concetti Chiave
- Il segmento AC è lungo 24,0 cm e B è il punto medio, con cariche positive poste in A, B e C.
- Le cariche sono: QA = 73,5 nC, QB = 18,1 nC, QC = 33,8 nC, tutte generano forze repulsive su QC.
- La forza elettrica tra A e C, calcolata con la legge di Coulomb, è 3,88 × 10-4 N.
- La forza elettrica tra B e C, anche calcolata con la legge di Coulomb, è 3,82 × 10-4 N.
- La forza totale su QC è la somma delle forze da A e B, risultando in 7,70 × 10-4 N.
Di seguito un esercizio in cui è dato un segmento di una certa lunghezza, nel cui punto medio è fissata una carica, assieme alle altre due cariche che si trovano nei suoi estremi. Andremo a calcolare la forza elettrica agente sulla carica del secondo estremo del segmento. Vediamo il testo dell'esercizio.
Testo dell'esercizio
Il segmentoSi determini la forza elettrica totale agente sulla carica posta in C.

Svolgimento dell'esercizio
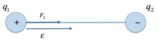
Dato che tutte le cariche sono positive, le due forze che agiscono suI moduli delle due forze si possono ricavare per mezzo della legge di Coulomb, e valgono:
Allo stesso modo si calcola anche la forza da B a C:
La forza totale è la somma di due vettori paralleli e con lo stesso verso. Quindi avrà stessa direzione, stesso verso delle due singole forze, e modulo dato dalla somma delle due:
Domande da interrogazione
- Qual è la lunghezza del segmento AC e quali sono le cariche poste nei punti A, B e C?
- Come si calcola la forza elettrica agente sulla carica in C?
- Qual è il valore della forza totale agente sulla carica in C?
Il segmento AC è lungo 24,0 cm. Nei punti A, B e C sono poste cariche puntiformi positive rispettivamente di 73,5 nC, 18,1 nC e 33,8 nC.
La forza elettrica su C è la somma delle forze repulsive dovute alle cariche in A e B, calcolate usando la legge di Coulomb. Le forze sono parallele e con lo stesso verso.
La forza totale agente sulla carica in C è 7,70 x 10^-4 N, risultante dalla somma delle forze F_{A,C} e F_{B,C}.

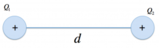





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo