Concetti Chiave
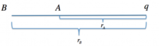
- L'esercizio analizza l'energia potenziale e il potenziale elettrico di due cariche opposte lungo un segmento di 30 cm.
- Calcola il potenziale elettrico in tre punti distinti: a 10 cm da q₁, nel punto medio e a 10 cm da q₂.
- Nel punto A, il potenziale elettrico risulta essere 1,8 x 10³ V, calcolato sommando le energie potenziali di q₁ e q₂.
- Nel punto medio del segmento, il potenziale è 0 V a causa delle cariche uguali in valore assoluto ma opposte in segno.
- Nel punto B, il potenziale è -1,8 x 10³ V, confermando la simmetria del sistema e le cariche opposte.
Questo appunto propone un esercizio svolto relativo ai concetti di energia potenziale e potenziale elettrico nel vuoto. In particolare studieremo casi diversi relativi ad un determinato sistema di due cariche, andando a calcolare il potenziale in tre punti distinti. Vediamo ora il testo dell'esercizio.
Testo dell'esercizio
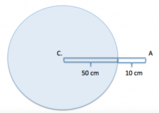
Due cariche- In un punto del segmento che dista [math] 10 cm [/math]dalla carica[math]q_1[/math];
- Nel punto medio del segmento;
- In un punto del segmento che dista [math] 10 cm [/math]dalla carica[math] q_2 [/math].

Svolgimento dell'esercizio
Calcoliamo l'energia potenziale nel puntoSi ha quindi:
Calcoliamo ora il potenziale in
Allo stesso modo, calcoliamo l'energia potenziale nel punto medio:
Il potenziale in tale punto sarà:
Calcoliamo ora l'energia potenziale nel punto
Il risultato non è sorprendente data la simmetria del problema. Infatti le cariche hanno valori uguali in modulo ma opposti in segno, e il problema risolto è molto simile a uno dei punti precedenti. Calcoliamo infine il potenziale in tale punto.
Il potenziale in tale punto sarà:
Domande da interrogazione
- Qual è il valore del potenziale elettrico nel punto che dista 10 cm dalla carica q1?
- Come si calcola il potenziale elettrico nel punto medio del segmento tra le due cariche?
- Qual è il potenziale elettrico nel punto che dista 10 cm dalla carica q2?
Il potenziale elettrico nel punto che dista 10 cm dalla carica q1 è 1,8 x 10^3 V.
Il potenziale elettrico nel punto medio è 0 V, poiché le cariche hanno valori uguali in modulo ma opposti in segno, annullandosi reciprocamente.
Il potenziale elettrico nel punto che dista 10 cm dalla carica q2 è -1,8 x 10^3 V.








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo