Concetti Chiave
- Il circuito contiene cinque resistori identici e una batteria da 45 V che fornisce 58 W di potenza.
- Le resistenze 3 e 4 sono in serie, quindi la loro resistenza equivalente è 2R.
- Le resistenze 2, 3-4 (in serie) e 5 sono in parallelo, con un equivalente di 2R/5.
- La resistenza equivalente dell'intero circuito è calcolata come 7R/5.
- Utilizzando la prima legge di Ohm e i dati forniti, la resistenza di ciascun resistore è 25 Ω.
In questo appunto risolveremo un esercizio che richiede di trovare il valore della resistenza di ciascun resistore che compone un circuito.
Prima di affrontare il problema è bene ricordare, siccome andremo a parlare di resistenze equivalenti, che:
se
sono in serie. Altrimenti:
se
sono in parallelo.
Queste relazioni ci torneranno utili a breve.
Testo del problema
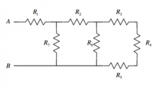
Il circuito in figura contiene cinque resistori identici.
La batteria da
fornisce una potenza di
Soluzione del problema
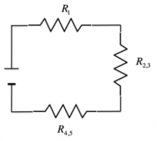
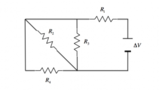
Consideriamo che le resistenze presenti nel circuito sono tutte uguali (perché per ipotesi sono identiche), calcoliamo la resistenza equivalente semplificando il circuito.
Sommiamo le resistenze 3 e 4 che sono in serie, troviamo che:
Ora sommiamo le resistenze
che sono in parallelo:
Calcoliamo ora la resistenza equivalente del circuito:
Sapendo che la potenza dissipata è data dalla formula
, possiamo ricavare con la formula inversa l'intensità di corrente che attraversa il circuito:
Infine applichiamo la prima legge di Ohm, la differenza di potenziale può essere espressa come
quindi la potenza sarà:
Per concludere sostituiamo i valori numerici all'espressione e ricaviamo il valore delle singole resistenze:
E andando a sostituire si ricava:
Domande da interrogazione
- Qual è la formula per calcolare la resistenza equivalente di resistori in serie e in parallelo?
- Come si calcola l'intensità di corrente nel circuito dato la potenza e la tensione?
- Qual è il valore della resistenza di ciascun resistore nel circuito?
La resistenza equivalente per resistori in serie è data da [math] R_{eq} = R_1 + R_2 [/math], mentre per resistori in parallelo è [math] \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} [/math].
L'intensità di corrente si calcola con la formula [math] i = \frac{P}{V} [/math], dove [math] P [/math] è la potenza e [math] V [/math] è la tensione. Nel problema, [math] i = \frac{58 W}{45 V} = 1,29 A [/math].
Il valore della resistenza di ciascun resistore nel circuito è [math] 25 \Omega [/math], calcolato utilizzando la formula [math] R = \frac{58 \cdot 5}{(1,29)^2 \cdot 7} [/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
