Concetti Chiave
- Il problema richiede di calcolare la resistenza equivalente tra due punti specifici di un circuito.
- Le resistenze R3, R4, e R5 sono in serie e sommate danno un totale di 6,00 Ω.
- Le resistenze in parallelo, R6 e la combinazione di R3, R4, R5, risultano in una resistenza totale di 2,00 Ω.
- Le resistenze R2 e la combinazione ottenuta (R3, R4, R5, R6) sono in serie, dando un totale di 8,00 Ω.
- La resistenza equivalente finale, considerando tutte le combinazioni, risulta essere 4,67 Ω.
In questo appunto andremo ad analizzare un problema che richiede di risolvere un circuito. In particolare viene chiesto di trovare la resistenza equivalente tra due punti del circuito. Procediamo intanto a leggere il testo dell'esercizio.
Testo dell'esercizio
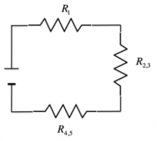
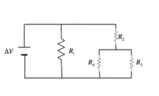
Calcolare la resistenza equivalente tra i punti A e B del circuito in figura.
Sono forniti i seguenti valori per le resistenze:
Svolgimento dell'esercizio
Per determinare la resistenza equivalente del circuito, cominciamo semplificando il circuito.
Ricordiamo che, in maniera informale, le resistenze in serie si sommano, le resistenze in parallelo sommano i reciproci.
Osserviamo quindi che, dato che le resistenze 3,4,5 che sono in serie, otteniamo:
.
Ora sommiamo le resistenze che sono in parallelo, ottenendo:
Successivamente, si può osservare che
sono in serie. Dunque si ottiene:
Sommiamo ora le resistenze
e
che sono in parallelo:
Infine, determiniamo la resistenza equivalente sommando le ultime due resistenze che sono in serie:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
