Concetti Chiave
- La resistenza equivalente di un circuito è calcolata come la somma di una resistenza in serie e due resistenze in parallelo.
- I valori specifici delle resistenze sono dati: R1 è 200 Ω, R2 è 600 Ω, R3 è 400 Ω, mentre R4 e R5 sono entrambi 120 Ω.
- Le resistenze R2 e R3 formano un parallelo, così come R4 e R5, contribuendo alla resistenza equivalente complessiva del circuito.
- La resistenza equivalente calcolata per il circuito è di 500 Ω, utilizzando la formula data e i valori delle resistenze.
- La differenza di potenziale del generatore è determinata usando la legge di Ohm, risultando in 220 V per il circuito.
Nel seguente appunto andremo ad affrontare un esercizio riguardante la resistenza equivalente di un circuito. Leggiamo ora il testo dell'esercizio.
Testo dell'esercizio
La resistenza equivalente di un circuito è data da
.
Supponi che i valori delle resistenze siano
,
,
,
e la corrente totale valga
.
- Disegnare il circuito corrispondente;
- Calcola il valore della differenza di potenziale del generatore presente nel circuito.
Svolgimento dell'esercizio
La resistenza equivalente è data dalla somma di tre addendi, e in particolare da tre resistenze che chiamiamo
,
e
Poiché sono sommate in questo modo, dobbiamo supporre che le tre resistenze siano in serie:
Sappiamo poi che
e
.
Possiamo scrivere quindi che:
Allo stesso modo:
Queste due resistenze sono quindi in parallelo e possiamo rappresentarle nel seguente modo:
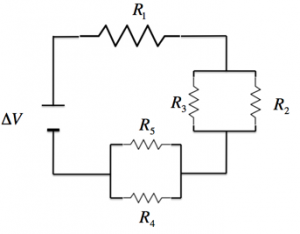
Per calcolare la differenza di potenziale del generatore, dobbiamo conoscere la resistenza equivalente del circuito; sostituiamo quindi i valori delle resistenze alla formula:
Svolgiamo i conti:
Infine applichiamo ora la prima legge di Ohm per trovare la differenza di potenziale:
Domande da interrogazione
- Qual è la formula per calcolare la resistenza equivalente di un circuito con resistenze in serie e parallelo?
- Come si calcola la differenza di potenziale del generatore nel circuito?
- Quali sono i valori delle resistenze e della corrente totale utilizzati nell'esercizio?
La resistenza equivalente è data da [math] R_{eq} = R_1 + \frac{R_2 \cdot R_3}{R_2 + R_3} + \frac{R_4 \cdot R_5}{R_4 + R_5} [/math], dove [math]R_1[/math] è in serie e [math]R_{2,3}[/math] e [math]R_{4,5}[/math] sono in parallelo.
La differenza di potenziale si calcola usando la prima legge di Ohm: [math] \Delta V = i \cdot R_{eq} [/math], dove [math]i[/math] è la corrente totale e [math]R_{eq}[/math] è la resistenza equivalente. Nel testo, [math] \Delta V = 220 V [/math].
I valori delle resistenze sono [math]R_1 = 200 \Omega[/math], [math]R_2 = 600 \Omega[/math], [math]R_3 = 400 \Omega[/math], [math]R_4 = R_5 = 120 \Omega[/math], e la corrente totale è [math]440mA[/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
