Qual è la resistenza equivalente del circuito in figura?

_francesca.ricci
di _francesca.ricci
1 min
Erectus
Vota
Appunto verificato
Contenuto verificato e approvato dal  Team di Esperti di Skuola.net Informazioni appunto verificato Informazioni appunto verificato hover

Risoluzione di un circuito, calcolo della resistenza equivalente e delle intensità  di corrente, applicazione della prima legge di Ohm

Concetti Chiave

  • Le resistenze R3 e R4 sono in parallelo con un valore equivalente di 20 Ω.
  • La somma delle resistenze R2 e R3,4 in serie è di 30 Ω.
  • Le resistenze R1 e R2,3,4 sono in parallelo per calcolare la resistenza equivalente finale.
  • La resistenza equivalente totale del circuito risulta essere 12 Ω.
  • Il calcolo coinvolge somme e frazioni per determinare la resistenza equivalente in serie e parallelo.

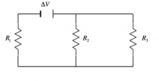
Qual è la resistenza equivalente del circuito in figura?

Le resistenze hanno i seguenti valori:

[math] R_1 = 20 â„&brv\bar; [/math]
[math] R_2 = 10 â„&brv\bar; [/math]

[math] R_3 = 60 â„&brv\bar; [/math]
[math] R_4 = 30 â„&brv\bar; [/math]

La differenza di potenziale vale:

[math] ∆V = 6 V [/math]

Risoluzione

Per determinare la resistenza equivalente del circuito, procediamo per gradi cercando di semplificare il circuito.

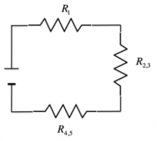
Per prima cosa, sommiamo le resistenze 3 e 4 che sono in parallelo:

[math] frac(1)(R_(3,4)) = frac(1)(R_3) + frac(1)(R_4) = [/math]

[math] frac(1)(60 â„&brv\bar;) + frac(1)(60 â„&brv\bar;) = frac(1 + 2)(60 â„&brv\bar;) = frac(1)(20 â„&brv\bar;) [/math]

[math] \to R_(3,4) = 20 â„&brv\bar; [/math]

risoluzione_circuito

Ora sommiamo le resistenze

[math] R_2[/math]
e
[math]R_(3,4) [/math]
e che sono in serie:

[math] R_(2,3,4) = R_(3,4) + R_2 = 20 â„&brv\bar; + 10 â„&brv\bar; = 30 â„&brv\bar; [/math]

Per trovare la resistenza equivalente del circuito basta determinare la resistenza equivalente fra le due rimaste, che sono in parallelo:

risoluzione_circuito

[math] frac(1)(R_(eq)) = frac(1)(R_1) + frac(1)(R_(2,3,4)) = [/math]

[math] frac(1)(20 â„&brv\bar;) + frac(1)(30 â„&brv\bar;) = frac(3 + 2)(60 â„&brv\bar;) = frac(1)(12 â„&brv\bar;) [/math]

[math] \to R_(eq) = 12 â„&brv\bar; [/math]
risoluzione_circuito

Domande da interrogazione

  1. Come si calcola la resistenza equivalente di un circuito con resistenze in parallelo e in serie?

    2. Per calcolare la resistenza equivalente, si sommano le resistenze in parallelo usando la formula \( \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} \) e poi si sommano le resistenze in serie direttamente. Nel testo, le resistenze \( R_3 \) e \( R_4 \) sono in parallelo, mentre \( R_2 \) è in serie con il risultato di \( R_3 \) e \( R_4 \).

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Vai al forum