Concetti Chiave
- La Legge di Ohm collega la differenza di potenziale, la resistenza e la corrente in un circuito elettrico.
- L'esercizio richiede di determinare la resistenza interna della batteria e la resistenza del resistore in un circuito con una forza elettromotrice di 7,0 V.
- Viene misurata una corrente di 90 mA e una differenza di potenziale di 6,0 V ai capi del resistore.
- La resistenza interna del circuito è calcolata usando la formula: r = (7,0 V - 6,0 V) / 90 mA, risultando in 11,1 Ohm.
- La resistenza del resistore è determinata con la formula R = V / i, risultando in 66,7 Ohm.
In questo appunto andremo a visualizzare un metodo risolutivo per un esercizio di elettromagnetismo. Ci viene richiesto di calcolare quanto valgono determinate resistenze, che determineremo utilizzando le leggi di Ohm.
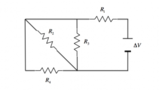
Vediamo ora il testo dell'esercizio:
Legge di Ohm
Essa mette in relazione la differenza di potenziale ai capi di un resistore con il valore della resistenza e l'intensità della corrente che passa attraverso il resistore stesso.Vale quindi:
[math] V = R \cdot i \longrightarrow R = \frac{V}{i} \longrightarrow i = \frac{V}{R} [/math]
dove le ultime due uguaglianze discendono dalla prima, passando alla formula inversa per ricavare
[math]i, V[/math]
.
Testo dell'esercizio
Una batteria di forza elettromotrice[math]7,0V[/math]
viene inserita in un circuito elettrico con un resistore. Si misurano la corrente elettrica e la differenza di potenziale ai capi del resistore e si trovano i valori [math] i = 90mA [/math]
e [math]V = 6,0 V[/math]
- Si determini la resistenza interna della batteria e la resistenza del resistore.
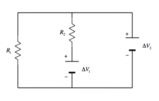
Svolgimento
La forza elettromotrice di un circuito data dalla formula[math] f_{em} = V + r \cdot i [/math]
. In effetti la forza elettromotrice è data dalla somma di due contributi, ovvero la differenza di potenziale ai capi del resistore e il prodotto tra la resistenza interna e l'intensità di corrente (segue dalla legge di Ohm).Possiamo da qui ricavare la resistenza interna del circuito:
[math] r = \frac{f_{em}-V}{r} \longrightarrow r = \frac{7,0 V - 6,0 V}{90 \cdot 10^{-3} A} = 11,1 Ohm[/math]
Ora sia
[math] R [/math]
la resistenza del resistore. Conosciamo che, sempre per la legge di Ohm, vale l'uguaglianza [math] V = R \cdot i [/math]
. Da questa uguaglianza discende, passando alla formula inversa, che:
[math] R = \frac{V}{i} = \frac{6 V}{90 mA} = \frac{6 V}{90 \cdot 10^{-3} A} = 66.7 Ohm [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
Appunto