Nel circuito nella figura si hanno i seguenti valori delle resistenze:.....

di _francesca.ricci

Ominide

2 min. di lettura

Vota

Concetti Chiave

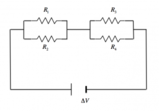
Il circuito è composto da varie resistenze: R1 = 5,0 Ω, R2 = R3 = 10 Ω, R4 = R5 = 20 Ω, R6 = 40 Ω, R7 = 30 Ω, con un generatore di 10V.
Le resistenze R3 e R4, R5 e R6 sono combinate in serie per ottenere R(3,4) = 30 Ω e R(5,6) = 60 Ω.
Le resistenze R(3,4) e R(5,6) sono poi combinate in parallelo per ottenere una resistenza equivalente R(3,4,5,6) = 20 Ω.
La resistenza totale del circuito è calcolata come R(eq) = 20 Ω, combinando R1 e la resistenza equivalente delle altre.
La corrente totale attraverso il circuito è 0,5 A e la differenza di potenziale ai capi di R7 è 7,5 V.

Nel circuito nella figura si hanno i seguenti valori delle resistenze:

[math]R_1 = 5,0 Î©[/math]

[math]R_2 = R_3 = 10 Î©[/math]

[math]R_4 = R_5 = 20 Î©[/math]

[math]R_6 = 40 Î©[/math]

[math]R_7 = 30 Î©[/math]

La differenza di potenziale ai capi del generatore è

[math]10V[/math]

Determina la resistenza equivalente del circuito.
Calcola il valore della corrente totale che attraversa il circuito.
Determina la differenza di potenziale ai capi di
[math]R_7 [/math]
.

Svolgimento

Punto 1

Risolviamo il circuito semplificandolo. Cominciamo sommando le resistenze 3 e 4, 5 e 6 che sono in serie:

[math] R_(3,4) = R_3 + R_4 = 10 Î© + 20 Î© = 30 Î©[/math]

[math] R_(5,6) = R_5 + R_6 = 20 Î© + 40 Î© = 60 Î©[/math]

circuito_equivalente

Ora sommiamo le resistenze

[math]R_(5,6)[/math]

[math]R_(3,4)[/math]

che sono in parallelo:

[math] frac(1)(R_(3,4,5,6)) = frac(1)(R_(3,4)) + frac(1)(R_(5,6)) = frac(1)(30 Î©) + frac(1)(60 Î©) = frac(1)(20 Î©)[/math]

[math] R_(3,4,5,6) = 20 Î© [/math]

circuito_equivalente

Sommiamo poi le resistenze

[math]R_2[/math]

[math]R_(3,4,5,6)[/math]

, che sono in serie:

[math] R_(2,3,4,5,6) = R_2 + R_(3,4,5,6) = 10 Î© + 20 Î© = 30 Î©[/math]

circuito_equivalente

Infine, sommiamo le resistenze

[math]R_7[/math]

[math]R_(2,3,4,5,6)[/math]

, che sono in parallelo:

[math] frac(1)(R_(2,3,4,5,6,7)) = frac(1)(R_7) + frac(1)(R_(2,3,4,5,6)) = frac(1)(30 Î©) + frac(1)(30 Î©) = frac(1)(15 Î©)[/math]

[math] R_(2,3,4,5,6,7) = 15 Î© [/math]

Possiamo ora determinare la resistenza equivalente del circuito:

circuito_equivalente

[math] R_(eq) = R_1 + R_(2,3,4,5,6,7) = 5,0 Î© + 15 Î© = 20 Î©[/math]

Punto 2

La corrente totale che attraversa il circuito può essere calcolata con la prima legge di Ohm:

Punto 3

Per risolvere il terzo punto, dobbiamo determinare la differenza di potenziale di

[math]R_(2,3,4,5,6,7)[/math]

, che è uguale alla differenza di potenziale di

[math]R_(2,3,4,5,6)[/math]

[math]R_7 [/math]

, poiché esse sono in parallelo.

Sapendo che l'intensità di corrente che attraversa

[math]R_(2,3,4,5,6,7)[/math]

è la stessa che attraversa l'intero circuito, possiamo scrivere che:

Domande da interrogazione

Qual è la resistenza equivalente del circuito?

Qual è il valore della corrente totale che attraversa il circuito?

La corrente totale che attraversa il circuito è [math]0,5 A[/math].

Qual è la differenza di potenziale ai capi di [math]R_7[/math]?

La differenza di potenziale ai capi di [math]R_7[/math] è [math]7,5 V[/math].

Nel circuito nella figura si hanno i seguenti valori delle resistenze:.....

Risoluzione di un circuito con resistenze in serie e in parallelo, calcolo della resistenza equivalente e della corrente totale