Concetti Chiave
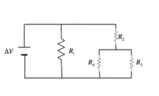
- Il resistore da 40 Ω è in parallelo con un resistore da 10 Ω, formando una resistenza equivalente di 8 Ω.
- La resistenza totale del circuito è calcolata in serie, risultando in 12 Ω, considerando anche un resistore da 4 Ω.
- La corrente totale nel circuito è di 1,5 A, calcolata dividendo la tensione totale di 18 V per la resistenza equivalente di 12 Ω.
- La differenza di potenziale attraverso i resistori in parallelo è di 12 V, condivisa tra i resistori da 40 Ω e 10 Ω.
- La potenza dissipata dal resistore da 40 Ω è 3,6 W, determinata utilizzando la formula P = i² * R con una corrente di 0,3 A.
Quale potenza dissipa il resistore da
Sono dati i seguenti valori delle resistenze e della tensione:
Risoluzione
Per determinare la potenza dissipata dal resistore da
, dobbiamo determinare l’intensità della corrente che attraversa quel resistore.
Cominciamo quindi semplificando il circuito e sommando le resistenza
e
che sono in parallelo:
Calcoliamo ora la resistenza equivalente del circuito sommando le due resistenze rimaste, che sono in serie:
Possiamo ora determinare l’intensità della corrente che attraversa il circuito, e quindi anche le resistenze
e
.
Possiamo calcolare la differenza di potenziale ai capi della resistenza
, che corrisponde alla differenza di potenziale delle resistenze 2 e 3, poiché esse sono in parallelo:
Applicando la prima legge di Ohm, possiamo determinare la corrente che attraversa
:
Per calcolare la potenza dissipata da questo resistore, applichiamo la formula
:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
