Matematica Maturità: analisi calcolo della matrici

Prepararsi con anticipo all' esame di maturità del liceo scientifico è fondamentale. Cominciare ad esercitarsi già da ora, quindi, è un'ottima strategia per arrivare pronti alla prova di matematica del 2015.

Può essere utile, quindi, ripassare i quesiti di matematica con l'analisi del calcolo matricale. Il prof di matematica, Francesco Bologna, ci spiega come affrontare tale quesito di matematica sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991EX.

Calcolo matriciale

Le indicazioni nazionali riguardanti gli obiettivi specifici di apprendimento dell'allievo del liceo hanno previsto che, al termine del percorso
liceale, lo studente dovrà conoscere i concetti salienti relativi al calcolo matriciale.

Nel paragrafo "Aritmetica e algebra" viene esplicitato che saranno ripresi e approfonditi i concetti di vettore, di dipendenza e indipendenza lineare, di prodotto scalare e vettoriale nel piano e nello spazio. E'
lasciata alla scelta dell'insegnante l'introduzione del calcolo matriciale.

In questo paragrafo affrontiamo l'analisi del calcolo matriciale.

Calcolo matriciale, come svolgerlo

In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi.

Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche
sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.

Esercizi:

Date le matrici

e

Calcola:

1. il determinante di

2. la matrice trasposta di

3. il prodotto

4. la somma e

5. calcolo della matrice inversa di

Esercizio 1.

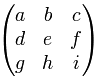
Considerata una matrice quadrata

il determinante lo possiamo calcolare tramite la formula di Sarrus:

Nel nostro caso si avrà:

Esercizio 2.

La matrice trasposta di una matrice è la matrice ottenuta scambiandone le righe con le colonne:

Esercizio 3.

Possiamo dire subito che e' un'operazione di composizione interna perchè il prodotto fra due matrici
quadrate dello stesso ordine e' ancora una matrice quadrata dello stesso ordine.

Esistono vari pprodotti tra matrici. Quello che viene usato normalmente e' il prodotto righe per colonne
indichiamolo con il simbolo

Per poter applicare tale metodo le matrici dovranno sempre avere lo stesso numero di colonne nella prima matrice del numero delle righe nella seconda.

Ad esempio il coefficiente

della matrice prodotto si otterrà nel seguente modo:

Nel nostro caso si avrà:

Esercizio 4.

In matematica, e più precisamente in algebra lineare, la somma fra matrici è l'operazione di addizione di due matrici

e con righe e colonne. Il risultato è una nuova matrice, che si indica con che possiede righe ed colonne.

Esercizio 5

Una matrice quadrata

si dice inversa della matrice quadrata

se vale la relazione:

Calcolare la matrice inversa di una matrice data e' un'operazione laboriosa che consta di numerosi calcoli.

Prima bisogna calcolare il valore del determinante della matrice, chiamiamolo

e vediamo se e' diverso da zero; se e' uguale a zero non esiste la matrice inversa.

Successivamente si calcola la trasposta della matrice di partenza.

Per ogni elemento della matrice trasposta calcolane il complemento algebrico, considerando il complemento algebrico (determinante del minore 2x2) come elemento ottieni una nuova matrice, chiamiamola

(si chiama matrice aggiunta).

Adesso dividi la matrice

per (cioe' dividi ogni termine per e ottieni l'inversa della matrice quadrata di partenza.

Quindi:

Il complemento algebrico di 2 sarà:

Quindi il primo coefficiente della matrice inversa sarà:

Procedendo allo stesso modo per gli altri coefficienti si avrà:

Vediamo come la calcolatrice FX991ES+ può rendere la procedura di calcolo molto semplice.

Passaggio #1

Attraverso al combinazione:

Collochiamoci nel menù MATRIX.

Passaggio #2

Digitiamo 1 e selezioniamo la matrice

Selezioniamo l'ordine della matrice

Passaggio #3

Tramite il tasto cursore inseriamo i valori:

Usciamo con il tasto AC.

Passaggio #4

Digitiamo

E digitiamo il tasto 2.

Potremo in tal modo, selezionando la matrice B, ripetere la procedura e memorizzare la seconda matrice.

Usciamo con il tasto AC.

Passaggio #5

Collochiamoci nel menù di calcolo tramite la combinazione:

Passaggio #6

Per calcolare il determinante della matrice A selezioniamo l'opzione 7.

Passaggio #7

Per inserire la matrice A, digitiamo la sequenza:

Passaggio #8

Per il calcolo della trasposta, ripetiamo la procedura digitando successivamente:

Passaggio #9

Per il calcolo della somma delle matrici o del loro prodotto basterà ripetere la procedura.

Digitiamo:

Per inserire la matrice A e

Per la matrice B.

Inserendo, attraverso il tasto cursore, le operazioni richieste si otterranno i risultati cercati:

Passaggio #10

Infine per il calcolo della matrice inversa, dopo aver inserito la matrice A con la solita sequenza:

Digitiamo:

Seguito da =. Otterremo banalmente la matrice inversa.

[youtube adv=no]gkpW2zXbu8g[/youtube]