Matematica - Soluzione problema 2 scientifico ordinario

di Daniele Grassucci

5 min

Autore

Pub: 19/06/2013 | Agg: 19/06/2013 17:15

Problema 2

Domanda 1

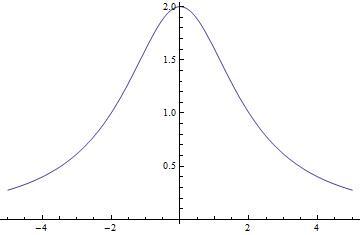
Funzione:

[math]f(x)=\frac8{4+x^2} [/math]

1. Il dominio della funzione:

[math]x\in(-\infty,+\infty).[/math]

2. La funzione è pari:

[math]f(x) = -f(-x)[/math]

. Quindì il grafico è
simmetrico rispetto all'asse y.

3. Punto di intersezione del grafico

[math]\Phi[/math]

con l'asse y:

[math]x=0\qquad\Rightarrow\qquad f(x) = 2.[/math]

Quind\`i il punto di intersezione del grafico

[math]\gamma[/math]

con l'asse y è (0,2).

4. Punto di intersezione del grafico

[math]\Phi[/math]

con l'asse x:

[math]f(x) = 0\qquad
\Rightarrow\qquad \mbox{impossibile}. [/math]

Quindì il grafico

[math]\Phi[/math]

non
interseca l'asse x.

5. Segno della funzione:

[math]f(x)>0 \qquad \Rightarrow \qquad x \in
(-\infty,+\infty).[/math]

Quindì la funzione è sempre positiva.

6. Limiti:

[math]\lim_{x\to\pm\infty}f(x) = 0. [/math]

7. Derivata:

[math]f'(x) = -\frac{16x}{(4+x^2)^2}[/math]

8. Segno della derivata:

[math]f'(x)>0 \qquad \Rightarrow \qquad x > 0,[/math]

[math]f'(x)>0 \qquad \Rightarrow \qquad x >0.[/math]

Quindì la funzione cresce nell'intervallo

[math]x\in(-\infty,0)[/math]

e
decresce nell'intervallo

[math]x\in(0,+\infty)[/math]

9. Punti critici:

[math]f'(x)=0 \qquad \Rightarrow \qquad x=0 \qquad - \qquad
\mbox{punto di massimo}[/math]

[math]f(0) = 2.[/math]

Il grafico

La tangente nel punto P:

[math] y=2+\frac{x}{2}[/math]

La tangente nel punto Q:

[math] y=2-\frac{x}{2}[/math]

Le tangenti si intersecano nel punto S(0,2). Quindì abbiamo un quandrilatero,
i vertici del quale hanno le coordinate: 0(0,0), P(-2,1), Q(2,1), S(0,2).
Possiamo trovare le lunghezze di tutti i lati:

[math]OP=\sqrt{(-2-0)^2+(1-0)^2}=\sqrt{5},\quad OQ=\sqrt{5},\quad
PS=\sqrt{5}, \quad SQ=\sqrt{5}[/math]

e anche dei diagonali:

[math]PQ=4, \quad OS=2[/math]

Vediamo che tutti i lati hanno la stessa lunghezza, quindì il quadrilatero
PSQO è un rombo. Avendo calcolato le lunghezze di tutti i segmenti, possiamo
ricavare i valori degli angoli:

[math] \cos SPO = \frac{OS^2 - PO^2 - SP^2}{2 PO SP} = -0.6[/math]

[math]\cos POQ = \frac{PQ^2 - PO^2 - QO^2}{2 PO QO} = 0.6[/math]

Da qui ricaviamo i valori degli angoli:

[math]SPO=126^{\circ} 8',
\quad POQ = 53^{\circ}8'.[/math]

--------------------------------------------------------------------

Domanda 2
L'equazione della retta t che passa per l'origine

[math]y=kx.[/math]

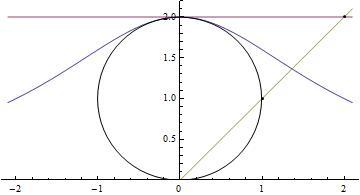
Matematica - Soluzione problema 2 scientifico ordinario articolo

L'equazione della circonferenza

[math]x^2 + (y-1)^2 = 1. [/math]

Il punto in cui la retta taglia la circonferenza possiamo trovare dal sistema

[math]\left\{
\begin{array}{l} y = kx \\ x^2 + (y-1)^2 = 1
\end{array}
\right. [/math]

la soluzione del quale ci permette di trovare le coordiante del punto A:

[math]A\,\left(\frac{2k}{k^2+1},\frac{2k^2}{k^2+1}\right). [/math]

Le coordinate del punto B troviamo risolvendo il sistema

[math]\left\{ \begin{array}{l} y = kx \\
y=2
\end{array}
\right. \Rightarrow \left\{\begin{array}{l} x = \frac2k \\
y=2
\end{array}
\right. [/math]

Qundi il punto B ha le coordinate

[math]B\,\left(\frac2k,2\right). [/math]

Se sostituiamo l'ascissa x di B e l'ordinata y di A nell'equazione della curva

[math]\Phi: \quad y=\frac8{4+x^2} [/math]

otteniamo un'equazione giusta, quindi questi valori sono un punto di

[math]\Phi[/math]

, qualunque sia la retta t.

-----------------------------

Domanda 3
L'area della regione R

[math]S_R=\int_0^2 f(x)dx = \int_0^2 \frac8{4+x^2}dx = 4\arctan \frac{x}2 \vert_0^2 = \pi. [/math]

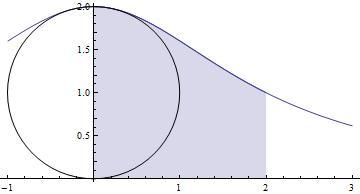
Matematica - Soluzione problema 2 scientifico ordinario articolo

Un cerchio di raggio r ha l'area

[math]S_r = \pi r^2 \quad \Rightarrow\quad S_r=S_R. [/math]

La regione tra

[math]\Phi[/math]

e tutto l'asse x

[math]S=\int_{-\infty}^{\infty} f(x)dx = \int_{-\infty}^{\infty} \frac8{4+x^2}dx = 4\arctan \frac{x}2 \vert_{-\infty}^{\infty} = 4\pi \quad \Rightarrow \quad S=4 S_r. [/math]

-------------------------------------

Domanda 4
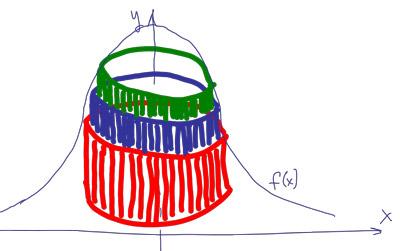
Il solido W possiamo rappresentare come un insieme dei ``tubi'' con l'asse y, con raggio interno x, esterno x+dx e di altezza f(x).
Il volume di ogni tubo è il prodotto dell'area della sua base e della sua altezza.
La base è un anello di raggio interno x ed esterno x+dx, quindi l'area è

[math]2\pi x dx[/math]

, mentre l'altezza è il valore della funzione nel punto x, cioè f(x).
Quindi il volume di ogni tubo uguale

[math]2\pi x dx f(x).[/math]

Il volume del solido W è la somma dei volimi di questi tubi, quindi è un integrale

[math]+V = \int_0^{\infty} 2\pi x dx f(x) =2\pi \int_0^{\infty} x f(x)dx[/math]

La spiegazione schematicamente possiamo illustrare con il disegno.

Matematica - Soluzione problema 2 scientifico ordinario articolo

News correlate

Matematica - Soluzione problema 1 scientifico ordinario

Matematica - Soluzione problema 2 scientifico PNI

Matematica - Soluzione problema 1 scientifico PNI

Matematica - Soluzioni quesiti scientifico ordinario