L'area di un triangolo rettangolo isoscele misura
[math]128 cm^2[/math]
.
Calcola il perimetro del triangolo.
Soluzione
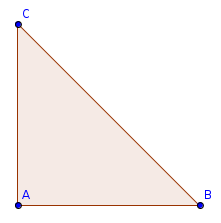
Dati
[math]ccA=128cm^2[/math]
[math]\bar(AB)=\bar(AC)[/math]
Svolgimento
L'area del triangolo è data dalla formula
[math]ccA=(\bar(AB) \cdot \bar(AC))/2=128 cm^2[/math]
Poniamo
[math]\bar(AB)=\bar(AC)=x[/math]
, e sostituendo si ha
[math](x^2)/2=128 cm^2[/math]
risolviamo la seguente equazione di secondo grado
[math](x^2)/2=128 cm^2[/math]
;
[math]x^2=2 \cdot 128 cm^2[/math]
;
[math]x^2=256 cm^2 -> x=\sqrt{256} cm=16 cm[/math]
.
Quindi
[math]\bar(AB)=\bar(AC)=16 cm[/math]
Per il Teorema di Pitagora si ha
[math]BC=\sqrt{(\bar(AB))^2+\bar(AC)^2}=\sqrt((16 cm)^2+(16 cm)^2)=\sqrt(256+256) cm=\sqrt(512)cm=22,63 cm[/math]
.
Pertanto
[math]2p=\bar(AB)+\bar(AC)+\bar(BC)=(16+16+22,63) cm=54.63 cm[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
