1) L'area cercata e' differenza tra l'area del settore circolare e quella del triangolo ABO
L'area del settore circolare, dal momento che l'area del cerchio e'
[math] \pi r^2 [/math]
inteso
[math] \pi [/math]
la meta' dell'angolo giro, si ricava, ad esempio, attraverso la proporzione
[math] \pi r^2: \pi= A: \frac{x}{2} [/math]
da cui
[math] A= \frac{xr^2}{2}[/math]
Del triangolo si sa che tale poligono e' isoscele (due lati sono r).
Per trovare l'area ci occorre la lunghezza del segmento AB e la relativa altezza.
Il segmento AB e' dato, per il teorema di Carnot, da:
[math]AB^2= r^2+r^2-2r^2 \cdot \cos x [/math]
da cui
[math]AB^2=2r^2 \cdot (1-\cos x) [/math]
L'altezza del triangolo sara', per il teorema di Pitagora, utilizzando il triangolo rettangolo meta' del triangolo isoscele
con base pari a metà di AB
[math] OC= \sqrt{r^2- \frac{r^2}{2} + \frac{r^2}{2} \cos x}=[/math]
[math] = \sqrt{ \frac{r^2}{2}(1+ \cos x)}= \frac{r}{ \sqrt{2}} \sqrt{1+ \cos x} [/math]
l'area del triangolo, quindi sara'
[math] A_{AOB}= \frac{1}{2} \cdot \frac{r}{ \sqrt{2}} \sqrt{1+ \cos x} \cdot \frac{2r}{ \sqrt{2}} \sqrt{1- \cos x}= [/math]
[math] = \frac{r^2}{2} \sqrt{1-cos^2} [/math]
che per la relazione fondamentale della trigonometria dara'
[math] \frac{r^2}{2} \cdot \sqrt{ \sin^2 x} [/math]
Trattandosi di un triangolo, x sara' senz'altro compresa tra
[math]0 [/math]
e
[math] \pi [/math]
e pertanto la semplificazione di radice non necessitera' del valore assoluto
[math] A_{AOB}= \frac{r^2}{2} \sin x [/math]
Pertanto l'area S compresa tra l'arco e la corda sara'
[math]S(x)= \frac{r^2x}{2}- \frac{r^2}{2} \sin x = \frac{r^2}{2} (x- \sin x)[/math]
(Altro modo per risolvere l'area del triangolo poteva essere, piu' semplicemente, valutare l'altezza relativa ad un lato del triangolo pari al raggio;
L'altezza relativa a tale lato, era, per la definizione di seno, data da:
[math] r \sin x [/math]
dal momento che il seno, per definizione, è il rapporto tra il cateto non adiacente l'angolo x e l'ipotenusa e quindi
[math] \frac{h}{r}= \sin x [/math]
)
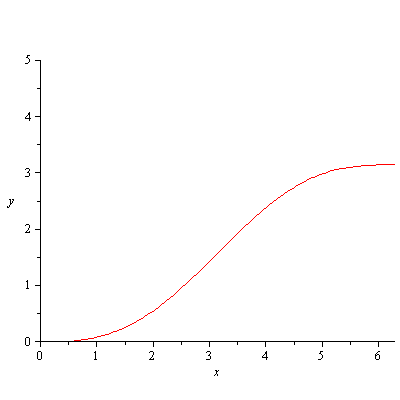
2)Studio della funzione
Intersezione con gli assi
[math] S(0)=0 [/math]
Dal momento che la funzione
[math] \sin x<x \forall x \in \mathbb{R}^+ [/math]
non esisteranno altri punti di intersezione con l'asse x.
Segno della funzione
[math] S(x)>0 \forall \ x \in D [/math]
La funzione e' limitata e definita su tutto il dominio, pertanto non esistono limiti.
Studio della derivata prima:
[math] S'(x)= \frac{1}{2}(1- \cos x) \ge 0 [/math]
[math]\cos x \ne 1 \ \forall x \in D [/math]
Pertanto
[math]S(x)[/math]
e' sempre crescente
Dal momento che la funzione è ristretta ed e' sempre crescente, in
[math]x=0[/math]
avremo un minimo assoluto di coordinate
[math](0,0)[/math]
e in
[math]2 \pi [/math]
un punto di massimo assoluto
[math]( 2 \pi, \pi) [/math]
Studio della derivata seconda
[math]S''(x)= \frac{ \sin x}{2} \ge 0[/math]
Da cui
[math]\sin x \ge 0 [/math]
e pertanto
[math] 0 \le x \le \pi \ U \ x=2 \pi [/math]
Concluderemo quindi che nell'intervallo
[math](0, \pi) [/math]
la funzione avrà concavita verso l'alto, nell'intervallo
[math]( \pi, 2 \pi) [/math]
verso il basso e nei punti
[math] 0 \ \pi \ \ 2 \pi[/math]
punti di flesso.
3) Uguagliata l'area del settore circolare trovata al punto 1 a
[math]100 m^2 [/math]
[math] A_{AOB}= \frac{1}{2}xr^2= 100 m^2 [/math]
si ricava
[math]x= \frac{200}{r^2}[/math]
Posto l l'arco di circonferenza AB ne calcoliamo la lunghezza in funzione di r(anche questo, ad esempio, tramite una proporzione)
[math] 2 \pi r: 2 \pi = l :x [/math]
Da cui
[math]l=xr[/math]
[math]P(r)= 2r + xr= 2r + \frac{200}{r}=2 (r+ \frac{100}{r})[/math]
Attraverso lo studio della derivata prima
[math]P'(r)=2(1- \frac{100}{r^2})[/math]
Otteniamo
[math]2(1- \frac{100}{r^2}) \ge 0[/math]
[math]\frac{r^2-100}{r^2} \ge 0[/math]
Il denominatore, sempre positivo, non partecipa allo studio del segno della frazione.
Posto pertanto
[math]r\ne 0 [/math]
[math]r^2-100 \ge 0[/math]
[math]r^2-100 \ge 0 [/math]
[math]r \le -10 \ U \ r \ge 10[/math]
[math]r \le -10 [/math]
non ha significato, trattandosi della lunghezza del raggio della circonferenza, pertanto l'unico intervallo sara'
[math] r \ge 10 [/math]
La funzione sara' decrescente nell'intervallo
[math](0, 10)[/math]
crescente in
[math]r > 10 [/math]
e pertanto avra' minimo per
[math]r=10[/math]
[math]P(10)=40 [/math]
[math]x= \frac{200}{r^2}=2 [/math]
che e' l'ampiezza dell'angolo espressa in radianti.
L'angolo
[math] \alpha [/math]
espresso in gradi, sara' dato da
[math] \alpha : 360^{ \circ}=x:2 \pi[/math]
[math] \alpha= \frac{360^{\circ}}{ \pi} \approx 114,59^{\circ}[/math]
4)
[math]r=2 \ \ x= \frac{ \pi}{3}[/math]
[math]0 \le x \le 2[/math]
dal momento che al più x potrà coincidere con il raggio.
Disegnata la situazione in un opportuno sistema di assi cartesiani, posto il raggio OB sull'asse delle ascisse e O sull'origine, il punto P avrà coordinate
[math]P(\alpha,0)[/math]
OA sarà la retta di pendenza
[math] \tan \frac{ \pi}{3}[/math]
e pertanto tutti i punti ad essa appartente (dal momento che passa per l'origine..) avranno coordinate
[math] ( \alpha, \sqrt{3} \alpha) [/math]
Il lato del quadrato, sarà pertanto
[math] \sqrt{3} \alpha [/math]
quando
[math]\alpha\le 1[/math]
, mentre per
[math]1\le \alpha\le 2[/math]
tale punto apparterrà all'arco di circonferenza di equazione
[math]x^2+y^2=4[/math]
e avrà coordinate
[math](\alpha,\sqrt{4-\alpha^2})[/math]
.
Il calcolo del volume del solido di rotazione sarà
[math] W= \int_0^2{l^2( \alpha)d \alpha}[/math]
[math]= \int_0^1{3 \alpha^2 d \alpha}+\int_1^2 (4-\alpha^2)\ d\alpha[/math]
[math]= [ \alpha^3]_0^1+[4\alpha-\alpha^3/3]_1^2=1+8-8/3-4+1/3=8/3[/math]
di 
