Matematica PNI - Soluzione primo problema

di Simone Milli

4 min

Autore

Pub: 26/06/2009 | Agg: 26/06/2009 14:31

Matematica PNI - Soluzione primo problema articolo

Punto 1

[math] f(x) = \left(1+x+\frac{x^2}{2!}+\ldots+\frac{x^n}{n!}\right) e^{-x} [/math]

[math] n \in \mathbb{N}, x\in \mathbb{R}[/math]

[math]f'(x) = \left(1+x+\ldots+\frac{nx^{n-1}}{n!}\right)e^{-x}-\left(1+x+\frac{x^2}{2!}+\ldots+\frac{x^n}{n!}\right)e^{-x}[/math]

[math]= -\left(1+x+\frac{x^2}{2!}+\ldots+\frac{x^{n-1}}{(n-1)!}\right)e^{-x}-\left(1+x+\frac{x^2}{2!}+\ldots+\frac{x^{n-1}}{(n-1)!}+\frac{x^n}{n!}\right)e^{-x}[/math]

[math]= -\frac{x^n}{n!}e^{-x}[/math]

Punto 2

[math]f'(x) = 0 \Leftrightarrow x = 0[/math]

Se n è pari =>

[math]f'(x) \leq 0 \forall x[/math]

Se n è dispari =>

[math]f'(x) > 0\ per\ x f'(x)0[/math]

Allora se n è pari => f sempre decrescente e non ha né massimo né minimo
se n è dispari allora:
f cresce per x f descresce per x>0
f ha un massimo in x = 0 e f(0) = 1 => M(0;1)

Ora

[math]\lim_{x\rightarrow + \infty} f(x) = \lim_{x\rightarrow + \infty} \frac{x^n}{n!}e^{-x}[/math]

(forma indeterminata

[math]0 \cdot \infty[/math]

)

[math]=\lim_{x\rightarrow + \infty} \frac{x^n}{n!e^x}[/math]

Applicando de l'Hopital n volte:

[math]=\lim_{x\rightarrow + \infty} \frac{n!}{n!e^x}=0^+[/math]

[math]=\lim_{x\rightarrow - \infty} f(x) = \pm \infty[/math]

(il segno dipende da n)

Infatti se n è dispari:

[math]\lim_{x\rightarrow - \infty} f(x) = \lim_{x\rightarrow - \infty} \frac{x^n}{n!}e^{-x}[/math]

.
Posto t = -x

[math]\lim_{t\rightarrow + \infty} \frac{(-1)^n t^n}{n!}e^{t}=\\
- \frac{1}{n!} \lim_{t\rightarrow + \infty} t^n e^t = - \infty[/math]

Allora se n è dispari M(0;1) è un massimo assoluto e quindi

[math]f(x) \leq 1[/math]

Punto 3) Se

[math]n=2[/math]

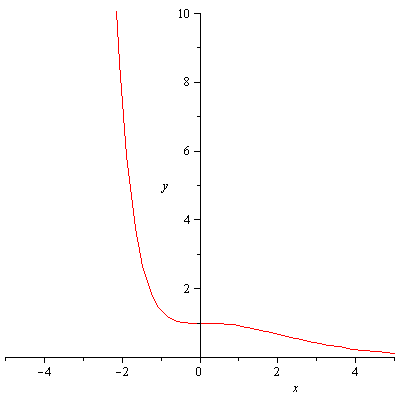
[math]g(x)=\left(1+x+\fra{x^2}{2}\right)e^{-x}=\frac{e^{-x}}{2}\left(x^2+2x+2)=\frac{e^{-x}}{2}[(x+1)^2+1][/math]

La funzione risulta sempre positiva non si annulla mai. Inoltre, se

[math]x=\Rightarrow g(0)=1[/math]

. Si ha poi

[math]\lim_{x\rightarrow-\infty}g(x)=\lim_{x\rightarrow-\infty}\frac{x^2\ e^{-x}}{2}=+\infty[/math]

[math]\lim_{x\rightarrow+\infty}g(x)=\lim_{x\rightarrow+\infty}\frac{x^2\ e^{-x}}{2}=0^+[/math]

[math]m=\lim_{x\rightarrow-\infty}\frac{g(x)}{x}=\lim_{x\rightarrow-\infty}\frac{x\ e^{-x}}{2}=-\infty[/math]

e quindi

[math]y=0[/math]

è un asintoto orizzontale a destra e non ci sono altri asintoti.

Avendosi poi

[math]g'(x)=-\frac{x^2}{2}\ e^{-x}[/math]

allora

[math]g'(x)\leq 0[/math]

per ogni

[math]x\in\mathbb{R}[/math]

. Per cui non ci sono estremi e la funzione risulta ovunque decrescente. Infine

[math]g''(x)=-\frac{1}{2}\left[2x e^{-x}-x^2 e^{-x}\right]=\frac{x e^{-x}}{2}(x-2)\geq 0[/math]

ed avendosi

[math]x\geq 0[/math]

[math]e^{-x}>0[/math]

per ogni valore reale e

[math]x-2\geq 0\Rightarrow x\geq 2[/math]

, abbiamo due flessi nei punti

[math](0,1),\ (2,5/e^2)[/math]

e la funzione rivolge la concavità verso l'alto su

[math](-\infty,0)\cup(2,+\infty)[/math]

Punto 4) Abbiamo:

[math]\int_0^2 g(x)\ dx=\int_0^2\frac{e^{-x}}{2}(x^2+2x+2)\ dx\\
=-\frac{e^{-x}}{2}(x^2+2x+2)|_0^2+\int_0^2\fra{e^{-x}}{2}(2x+2)\ dx\\
=-\frac{5}{e^2}+1+\left[-\frac{e^{-x}}{2}(2x+2)|_0^2+\int_0^2\frac{e^{-x}}{2}\cdot 2\ dx\right]\\
=-\frac{5}{e^2}+1-\frac{3}{e^2}+1-e^{-x}|_0^2=2-\frac{8}{e^2}-\frac{1}{e^2}+1=3-\frac{9}{e^2}.[/math]

L'integrale rappresenta l'ara sottesa dalla curva

[math]g(x)[/math]

, delimitata dall'asse delle ascisse e dalle rette di equazione

[math]x=0,\ x=2[/math]

News correlate

Matematica PNI - Soluzione secondo problema

Matematica tradizionale - Soluzione Primo Problema

Matematica - Soluzione 2. quesito ordinario e PNI

Matematica tradizionale - Soluzione secondo problema