Studio del grafico di una funzione

1. Dominio Il dominio di una funzione è il più grande sottoinsieme di mathbb{R} nel quale l'espressione analitica della fuzione non perde di significato. f(x)=1/g(x) dominio g(x) e0...
_Tipper
di Gianni Sammito
Autore
14 min
x2.png

Indice

  1. Dominio[/2h]
    1. Esempi
  2. Simmetrie
  3. Proprietà
    1. Esempio
  4. Periodicità
    1. Esempio
  5. Intersezione con gli assi
    1. Esempio
  6. Studio del segno
    1. Esempio
    2. Asintoti verticali
    3. Esempio
    4. Asintoti orizzontali
    5. Esempio
  7. Asintoti obliqui
    1. Esempio
  8. Derivata prima
    1. Punto angoloso
    2. Flesso a tangente verticale
  9. Derivata seconda

Dominio[/2h]

Il dominio di una funzione è il più grande sottoinsieme di

[math]\mathbb{R}[/math]

nel quale l'espressione analitica della fuzione non perde di significato.

[math]f(x)=1/g(x)[/math]

dominio

[math]g(x) \ne 0[/math]

[math]f(x) = \sqrt[n]{g(x)}[/math]

n pari, dominio

[math]g(x)>=0[/math]

[math]f(x)=\log(g(x))[/math]

dominio

[math]g(x)>0[/math]

[math]f(x)=\tan(g(x))[/math]

dominio

[math]g(x) \neq \frac{\pi}{2} + k \cdot \pi, \quad k \in \mathbb{Z}[/math]

[math]f(x) = \cot(g(x))[/math]

dominio

[math]g(x) \neq k \cdot \pi, \quad k \in \mathbb{Z}[/math]

[math]f(x)=a\sin(g(x))[/math]

dominio

[math]-1<=g(x)<=1[/math]

[math]f(x)=a\cos(g(x))[/math]

dominio

[math]-1<=g(x)<=1[/math]

Esempi

il dominio massimale della funzione

[math]f(x) = \sqrt{x - 1}[/math]

è

[math]\text{dom}(f) = {x \in \mathbb{R}: x \ge 1}[/math]

,

[math]g(x) = \frac{1}{x}[/math]

è

[math]\text{dom}(g) = {x \in \mathbb{R}: x \ne 0}[/math]

.

Vuoi lavorare nella creatività? All’Istituto Pantheon il placement è del 100% Vuoi lavorare nella creatività? All’Istituto Pantheon il placement è del 100%

Simmetrie

Una funzione

[math]f[/math]

, definita su un dominio simmetrico rispetto all'origine, si dice pari se e solo se risulta

[math]f(-x) = f(x)[/math]

per ogni

[math]x \in \text{dom}(f)[/math]

. Una funzione

[math]f[/math]

, definita su un dominio simmetrico rispetto all'origine, si dice dispari se e solo se risulta

[math]f(-x) = -f(x)[/math]

per ogni

[math]x \in \text{dom}(f)[/math]

.

Il grafico di una funzione pari è simmetrico rispetto all'asse

[math]y[/math]

, mentre il grafico di una funzione dispari è simmetrico rispetto all'origine. Questo vuol dire che per tracciare il grafico di una funzione a simmetria pari, o dispari, è sufficiente studiarlo per le

[math]x[/math]

positive del dominio, estendendolo poi per simmetria alle

[math]x[/math]

negative del dominio.

Ovviamente non è detto che ogni funzione sia pari o dispari, ci sono funzioni che non sono né pari né dispari. Ad esempio una funzione con un dominio non simmetrico rispetto all'origine non può essere né pari né dispari.

Proprietà

- il prodotto, o il rapporto, di due funzioni pari è una funzione pari
- il prodotto, o il rapporto, di due funzioni dispari è una funzione pari
- il prodotto, o il rapporto, di una funzione pari con una funzione dispari è una funzione dispari
- la somma di due funzioni pari è una funzione pari
- la somma di due funzioni dispari è una funzione dispari
- la somma di una funzione pari con una dispari è una funzione, in generale, né pari né dispari

Esempio


[math]f(x)=x^2[/math]

è una funzione pari,

[math]f(-x)=f(x)[/math]

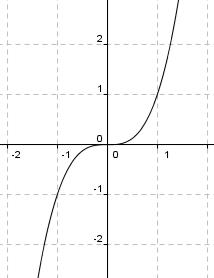
x3.png

[math]f(x)=x^3[/math]

è una funzione dispari,

[math]f(-x)=-f(x)[/math]

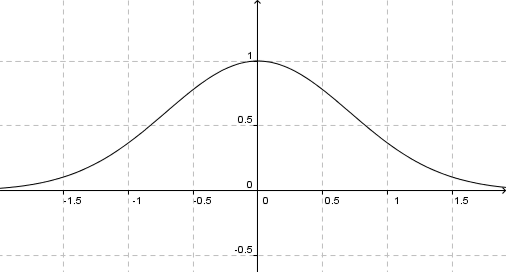
e-x2.png

[math]f(x) = e^{-x^2}[/math]

è pari
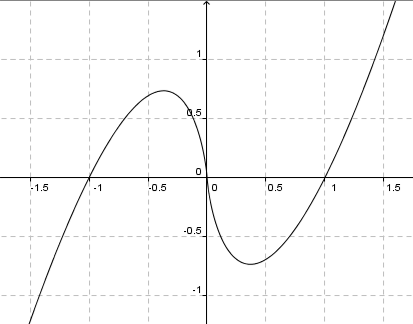
xlnx2.png

[math]f(x) = x \cdot ln(x^2)[/math]

è dispari,
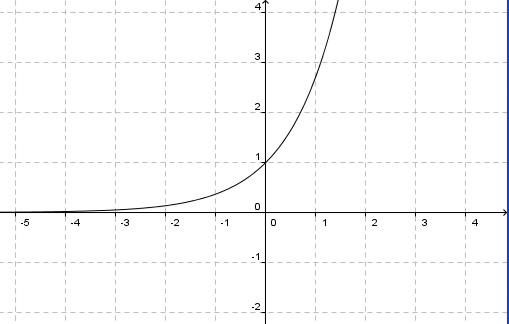
ex.png

[math]f(x) = e^x[/math]

non è né pari né dispari.

Periodicità

Una funzione è periodica di periodo T se

[math]f(x+T)=f(x)[/math]

. Sono periodiche le funzioni goniometriche e alcune funzioni composte da funzioni goniometriche.

Esempio

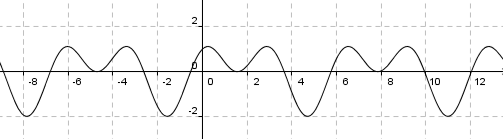
sinxcos2x.png

[math]f(x)=\sin(x) \cdot \cos(2x)[/math]

è periodica di periodo

[math]2 \cdot \pi[/math]

Intersezione con gli assi

Data una funzione

[math]f[/math]

, se

[math]0[/math]

appartiene al dominio allora il grafico di

[math]f[/math]

interseca l'asse

[math]y[/math]

nel punto

[math](0, f(0))[/math]

. Le intersezioni con l'asse

[math]y[/math]

possono essere al massimo una.

Per determinare le (eventuali) intersezioni con l'asse

[math]x[/math]

è sufficiente risovlere l'equazione

[math]f(x) = 0[/math]

. Se

[math]x_1, x_2, \ldots, x_n[/math]

sono le soluzioni dell'equazione, allora i punti di intersezione fra l'asse

[math]x[/math]

e il grafico di

[math]f[/math]

sono

[math](x_1, 0) \qquad (x_2, 0) \qquad \ldots \qquad (x_n, 0)[/math]

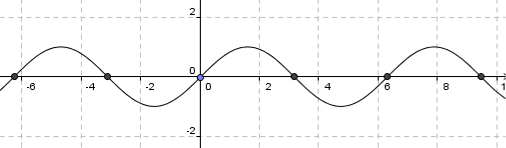
Esempio

la funzione

[math]f(x) = \sin (x)[/math]

interseca l'asse

[math]y[/math]

in

[math](0, \sin (0))[/math]

, cioè

[math](0,0)[/math]

, e interseca l'asse

[math]x[/math]

nei punti

[math](k \pi, 0)[/math]

, con

[math]k \in \mathbb{Z}[/math]

. Infatti le soluzioni di

[math]\sin (x)[/math]

sono date da

[math]x = k \pi, \quad k \in \mathbb{Z}[/math]

. sinx.png

Studio del segno

Studiare il segno di una funzione

[math]f[/math]

significa risolvere la disequazione

[math]f(x) ge 0[/math]

. In questo modo negli intervalli in cui la disequazione è soddisfatta la funzione è positiva, ossia il grafico si trova nel semipiano

[math]y \ge 0[/math]

, mentre negli intervalli (contenuti nel dominio) in cui la disequazione non è soddisfatta la funzione è negativa, ed il grafico si trova nel semipiano

[math]y < 0[/math]

.

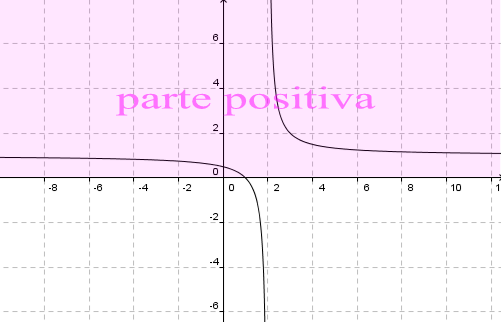
Esempio

La funzione

[math]f(x) = \frac{x-1}{x-2}[/math]

è positiva (o meglio, non negativa) per

[math]x \le 1 \quad \vee \quad x > 2[/math]

, mentre è negativa per

[math]1 < x < 2[/math]

. x-1dx-2positiva.png

Asintoti verticali

Quando una funzione ammette limite

[math]+\infty[/math]

o

[math]-\infty[/math]

in un punto

[math]x_0[/math]

, si dice che essa ha come asintoto verticale la retta

[math]x = x_0[/math]

.

Più precisamente, data una funzione

[math]f(x)[/math]

,

se

[math]\lim_{x \to x_0^-} f(x) = +\infty[/math]

(o

[math]-\infty)[/math]

, allora la retta

[math]x = x_0[/math]

è un asintoto verticale sinistro;

se

[math]\lim_{x \to x_0^+} f(x) = +\infty[/math]

(o

[math]-\infty)[/math]

, allora la retta

[math]x = x_0[/math]

è un asintoto verticale destro;

se

[math]\lim_{x \to x_0} f(x) = +\infty[/math]

(o

[math]-\infty)[/math]

, allora la retta

[math]x = x_0[/math]

è un asintoto verticale (sia destro che sinistro).

In sostanza si determina l'esistenza di asintoti verticali calcolando i limiti (della funzione) per i punti appartenenti alla frontiera del dominio.

Notare che il grafico di una funzione non può intersecare in nessun punto gli asintoti verticali.


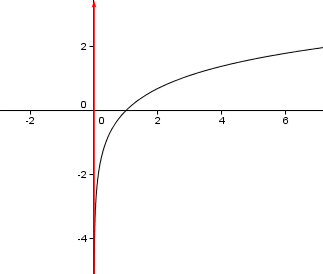
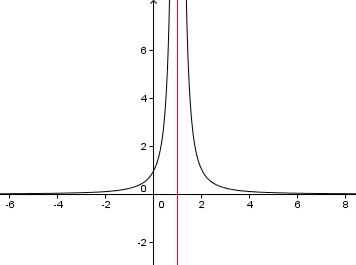
Esempio

Data la funzione

[math]f(x) = \ln(x)[/math]

, la retta

[math]x = 0[/math]

è un asintoto verticale destro, infatti

[math]\lim_{x \to 0^+} \ln(x) = -\infty[/math]

.
logx-asintoto.png

Data la funzione

[math]g(x) = \frac{1}{(x-1)^2)}[/math]

, la retta

[math]x=1[/math]

è un asintoto verticale (destro e sinistro), infatti

[math]\lim_{x \to 1} \frac{1}{(x-1)^2} = +\infty[/math]

. 1sux-1.png

Asintoti orizzontali

Per determinare l'esistenza di eventuali asintoti orizzontali di una funzione

[math]f(x)[/math]

è necessario calcolare i limiti per

[math]x \to +\infty[/math]

o

[math]x \to -\infty[/math]

(ovviamente se il dominio è superiormente o inferiormente illimitato, rispettivamente, altrimenti tali limiti non esisterebbero).

Se

[math]\lim_{x \to +\infty} f(x)[/math]

esiste finito, e il risultato è

[math]k_1[/math]

, allora la retta

[math]y = k_1[/math]

è un asintoto orizzontale destro per il grafico di

[math]f[/math]

.

Analogamente se

[math]\lim_{x \to -\infty} f(x)[/math]

esiste finito, e il risultato è

[math]k_2[/math]

, allora la retta

[math]y = k_2[/math]

è un asintoto orizzontale sinistro per il grafico di

[math]f[/math]

.

Dopo aver trovato eventuali asintoti orizzontali, è utile calcolare le (eventuali) intersezioni del grafico della funzione con tali asintoti.

Se

[math]\lim_{x \to \pm \infty} f(x)[/math]

non esistono, o sono infiniti, allora la funzione non ammette asintoti orizzontali.

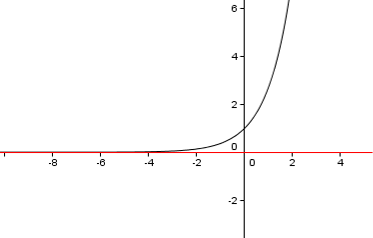
Esempio

La retta

[math]y = 0[/math]

è un asintoto orizzontale sinistro per la funzione

[math]f(x) = e^x[/math]

, infatti

[math]\lim_{x \to -\infty} e^x = 0[/math]

. ex-asintoto-oriz.png

Asintoti obliqui

Data una funzione

[math]f(x)[/math]

, se il limite per

[math]x \to +\infty[/math]

(rispettivamente

[math]x \to -\infty[/math]

) esiste ma non è finito, ci si può chiedere se per

[math]x \to +\infty[/math]

(rispettivamente

[math]x \to -\infty[/math]

) la funzione ammetta un asintoto obliquo.

Se

[math]\lim_{x \to +\infty} \frac{f(x)}{x} = m[/math]

esiste finito e non nullo, e se

[math]\lim_{x \to +\infty} f(x) - mx = q[/math]

esiste finito, allora la funzione

[math]f[/math]

ammette per

[math]x \to +\infty[/math]

un asintoto obliquo di equazione

[math]y = mx + q[/math]

.

Per

[math]x \to -\infty[/math]

la situazione è analoga.

Anche in questo caso, dopo aver determinato gli eventuali asintoti obliqui, può essere utile cercare (eventuali) intersezioni fra il grafico di

[math]f[/math]

e tali asintoti.

Esempio

La funzione

[math]f(x) = \frac{x^2-1}{x}[/math]

ammette come asintoto obliquo la retta

[math]y = x[/math]

, infatti

[math]\lim_{x \to \pm \infty} \frac{f(x)}{x} = 1[/math]

, e

[math]\lim_{x \to \pm \infty} f(x) - x = 0[/math]

. x2-1dx.png

Derivata prima

Una volta calcolata la derivata prima

[math]f'(x)[/math]

, è utile classificare i punti di non derivabilità in cui la funzione è continua (punti angolosi, flessi a tangente verticale, cuspidi).

Punto angoloso

se

[math]\lim_{h \to 0^-} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

e

[math]\lim_{h \to 0^+} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

esistono finiti ma diversi, allora

[math](x_0, f(x_0))[/math]

è un punto angoloso.

Flesso a tangente verticale

se

[math]\lim_{h \to 0^-} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

e

[math]\lim_{h \to 0^+} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

esistono, sono infiniti, e sono uguali, allora

[math](x_0, f(x_0))[/math]

è un punto di flesso a tangente verticale e

[math]x = x_0[/math]

è una retta tangente al grafico di

[math]f[/math]

che attraversa il grafico stesso.

Cuspide

se

[math]\lim_{h \to 0^-} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

e

[math]\lim_{h \to 0^+} \frac{f(x_0 + h) - f(x_0)}{h}[/math]

esistono, entrambi infiniti, ma diversi, allora

[math](x_0, f(x_0))[/math]

è un punto di cuspide.

Fatto questo si risolve l'equazione

[math]f'(x) = 0[/math]

, trovando così i punti critici, e si studia il segno di

[math]f'[/math]

. Un punto critico

[math]x_0[/math]

, in base al segno di

[math]f'[/math]

, si può classificare nel seguente modo
- se la derivata prima è negativa in un intorno sinistro di

[math]x_0[/math]

e positiva in un intorno destro di

[math]x_0[/math]

, allora

[math](x_0, f(x_0))[/math]

è un punto di minimo relativo
- se la derivata prima è positiva in un intorno sinistro di

[math]x_0[/math]

e negativa in un intorno destro di

[math]x_0[/math]

, allora

[math](x_0, f(x_0))[/math]

è un punto di massimo relativo
- se la derivata prima assume lo stesso segno in un intorno completo di

[math]x_0[/math]

, allora

[math](x_0, f(x_0))[/math]

è un punto di flesso a tangente orizzontale

Derivata seconda

Se la funzione considerata è sufficientemente regolare, è possibile calcolarne la derivata seconda, avendo così informazioni su flessi, concavità e convessità. Risolvendo l'equazione

[math]f''(x) = 0[/math]

si trovano i punti di flesso a tangente obliqua.

Fatto questo può essere utile studiare il segno della derivata seconda; negli intervalli in cui risulta

[math]f''(x) > 0[/math]

la funzione è convessa, invece negli intervalli in cui risulta

[math]f''(x) < 0[/math]

la funzione è concava.

News correlate

Skuola | TV
Play
E ADESSO? La verità su cosa fare dopo la maturità

Rivedi lo speciale di Skuola.net e Gi Group dedicato a tutti i maturandi che vogliono prendere una decisione consapevole sul proprio futuro grazie ai consigli di esperti del settore.

24 giugno 2025 ore 16:00

Segui la diretta