
Ecco su questa pagina la Soluzione della seconda prova maturità 2016 matematica: primo problema
Il grande giorno della Seconda prova di Maturità del 2016 è arrivato e non ci sta più tempo per ripassare, seguendo quello della prima prova di Maturità del 2016 di ieri. Ciò che è fatto è fatto, e scommetto che anche tu in questo momento stai pensando che avresti dovuto prepararti di più per questa seconda prova. Anche per la prima prova di Maturità 2016 è andata così, vero? D'altronde, il primo problema mette sempre un po’ in difficoltà, ma non fermarti alle apparenze. Procedi lentamente, cerca di capire bene la traccia e ragiona con calma. Se proprio non ce la fai, continua a leggere questo articolo e troverai la soluzione a tutti i tuoi problemi (letteralmente!).
Pensavi davvero che ti avremmo lasciato da solo per la maturità del 2016? I nostri tutor di matematica si sono impegnati quanto te nello svolgimento delle soluzioni del primo problema di matematica, quindi adesso sta a te essere furbo e riuscire a non farti beccare. Se stai semplicemente ricontrollando la soluzione per avere una conferma di ciò che hai scritto, non entrare nel panico se non la trovi. Hai ancora speranze con il secondo problema.
Ma bando alle ciance, eccoti dunque le soluzioni del primo problema della seconda prova di Matematica per il liceo scientifico e per il liceo delle Scienze applicate:
Le tre funzioni proposte sono
PUNTO 1
Affinché la funzione descriva il profilo del serbatoio deve soddisfare principalmente due condizioni:
1) non deve essere derivabile nel punto
,
2) dev'essere
Si vede facilmente che la
risulta derivabile in
e dunque non assume forma spigolosa, ma liscia.
Invece la
si annulla nei punti
solo per
, ma per questo valore non vengono soddisfatte le ulteriori richieste sulla funzione. Ad esempio calcolando
nell'intervallo
:
questa si annulla nei punti:
La derivata prima è una parabola con concavità verso il basso e due zeri compresi tra
e
, quindi cambia di segno. Di conseguenza la funzione non risulta monotona, come invece deve evidentemente essere dato il disegno fornito dall'amministratore.
La funzione giusta è quindi la
.
PUNTO 2
Data quindi
serve trovare un valore di
tale che il volume totale del serbatoio sia almeno di
. Troviamo dunque la formula del volume.
Dato che f è una funzione pari (risulta facilmente che
), si può restringere lo studio all'intervallo
.
L'area della superficie frontale del serbatoio, in funzione di
è dunque data dall'integrale definito della funzione nell'intervallo
moltiplicato per due:
Moltiplicando per la profondità si ottiene il volume:
Bisogna trovare il valore di k tale che
. E dunque
Non resta che verificare la condizione sull'angolo. Scelto come
, il primo valore intero maggiore di
, la funzione diventa:
la cui derivata, restringendosi all'intervallo
, è
La funzione in
assume un coefficiente angolare pari a
, che corrisponde ad un'inclinazione di
. Per cui anche la condizione sull'angolo risulta verificata.
PUNTO 3
Per determinare l'espressione del volume, concentriamoci nuovamente sulla semi-superficie da
a
.
In corrispondenza della quota
raggiunta dal liquido, ci accorgiamo che la superficie può essere divisa in due sezioni:
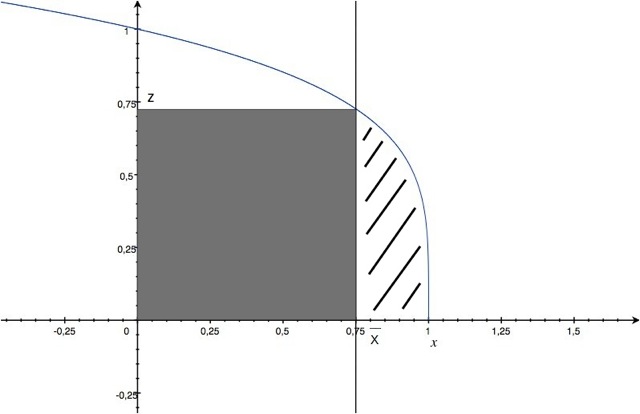
una parte rettangolare di base
ed altezza
, ed una parte sottesa dalla funzione
nell'intervallo
.
Per trovare l'espressione del punto
in funzione di
, risolviamo:
Calcoliamo la sezione sottesa dalla funzione tramite l'integrale definito:
La superficie totale da considerare è data dal precedente integrale più l'area del rettangolo. Quindi si ottiene:
ed il volume percentuale in funzione di z è:
in cui si intende:
PUNTO 4: OBIEZIONE DELL'AMMINISTRATORE
L'obiezione mossa dall'amministratore si può riassumere matematicamente evidenziando che egli si aspetta che il volume sia direttamente proporzionale all'altezza raggiunta dal gasolio (
). Solo in questo caso, infatti, la quantità percentuale dell'una grandezza coincide con quella della seconda.
Invece l'espressione del volume percentuale
ottenuta al precedente punto non è direttamente proporzionale a
, come evidenziato dal grafico delle due funzioni.
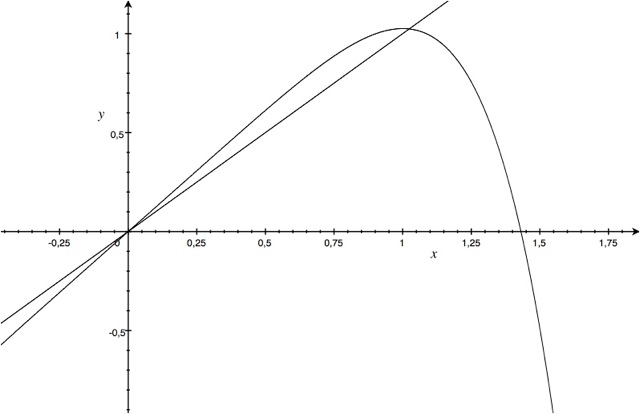
Dove la retta corrisponde a
e la curva a
.
L'errore che si commette è la differenza tra le due espressioni percentuali:
Il suo massimo si calcola imponendo la derivata prima uguale a
:
e verificando che la derivata seconda nel punto è negativa:
Soluzione a cura di Roberta Coletti e Matteo Del Prete







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo