Soluzioni seconda prova 2016 maturità scientifico: i quesiti di matematica

Soluzione della seconda prova di maturità di Matematica per il liceo scientifico. Qui troverete le soluzioni dei quesiti di matematica per il liceo scientifico e per il liceo delle Scienze applic...
melody_gio
di giorgia m.
Autore
17 min lettura
Questo articolo contiene un allegato
Soluzioni seconda prova 2016 maturità scientifico: i quesiti di matematica scaricato 367 volte
Download
Seconda prova di Maturità 2016 per il liceo scientifico sui quesiti di matematica

Ecco la soluzione delle tracce di Maturità 2016 della Seconda prova di maturità 2016 relativa ai quesiti del liceo scientifico e del liceo delle scienze applicate.

Il giorno della seconda prova di Maturità del 2016 di maturità è arrivato ed è tempo di dimostrare che siete in grado di svolgere almeno cinque dei dieci quesiti proposti. Cinque, sei, ma anche di più! Dovete dimostrare di aver davvero imparato qualcosa nell’arco di questi cinque anni scolastici, o almeno fare finta di averlo fatto.
Siete pronti? Ci siamo noi ad aiutarvi a fingere.
E’ una fortuna che i nostri tutor si siano impegnati per tutti voi maturandi dello scientifico e abbiano cercato in tempo reale le soluzioni ai vostri quesiti. Siete a metà del vostro percorso di maturità e non è proprio il caso di abbandonare adesso, quindi forza e coraggio, sguardo attento, mano lesta e copiate tutto ciò che vi serve per superare al meglio anche questa prova.
Mi raccomando però, non fatevi beccare o i quesiti saranno l’ultimo dei vostri problemi.

Le soluzioni dei quesiti li trovate qui di seguito!

Quesito numero 1

[math]\int_{- \infty}^{+\infty} \hspace{0,3cm} e^{-x^{2}}dx = \sqrt{\pi}[/math]

[math]\int_{- \infty}^{\cup} \hspace{0,3cm} e^{-x^{2}}dx = 1[/math]

Poiché

[math] e^{-x^{2}}[/math]
è una funzione pari, e
[math]\int_{- \infty}^{+\infty} \hspace{0,3cm} e^{-x^{2}}dx \simeq 1,77[/math]
, allora
[math]\cup[/math]
deve essere positivo dato che 1 è maggiore di
[math]\frac{1,77}{2}[/math]
.

A =

[math]\int_{- \cup}^{\cup} \hspace{0,3cm} x^{7}e^{-x^{2}}dx = 0 \hspace{2cm}[/math]
Poiché la funzione integranda è dispari.

B =

[math]\int_{- \cup}^{\cup} \hspace{0,3cm} e^{-x^{2}}dx = \int_{- \infty}^{\cup} \hspace{0,3cm} e^{-x^{2}}dx \hspace{0,2cm} - \int_{-\infty}^{- \cup} \hspace{0,3cm} e^{-x^{2}}dx = 1 - \int_{\cup}^{+ \infty} \hspace{0,3cm} e^{-x^{2}}dx = 1 - (\sqrt{\pi} - 1) = 2 - \sqrt{\pi}[/math]

C =

[math]\int_{-\infty}^{+\infty} \hspace{0,3cm} e^{-5x^{2}}dx[/math]

Ricordiamo che dall'integrale di Gauss

[math]\int_{- \infty}^{+\infty} \hspace{0,3cm} e^{-x^{2}}dx = \sqrt{\pi}[/math]
si ricava che
[math]\int_{- \infty}^{+\infty} \hspace{0,3cm} (e^{-x^{2}})^{a}dx = \frac{\sqrt{\pi}}{\sqrt{a}}[/math]

Allora

[math]\int_{- \infty}^{+\infty} \hspace{0,3cm} e^{-5x^{2}}dx = \frac{\sqrt{\pi}}{\sqrt{5}}[/math]

Panico Maturità? Entra sul canale Telegram dei maturandi Panico Maturità? Entra sul canale Telegram dei maturandi

Quesito numero 2

[math]y = 1 - ax^2 \hspace{2cm}[/math]
a > 0

[math]V (-\frac{b}{2a}, \hspace{0,2cm} -\frac{\Delta}{4a}) \hspace{1cm} V (0,1)[/math]

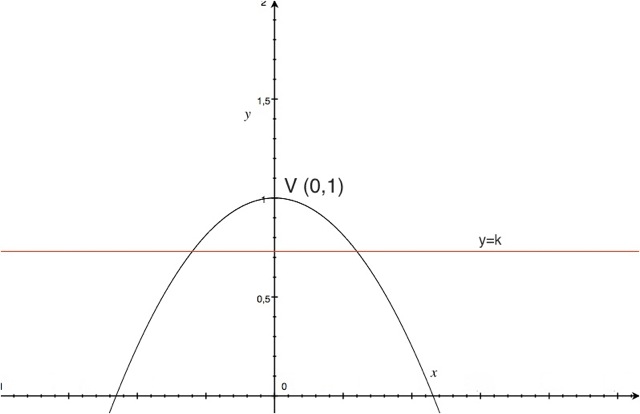
Soluzioni seconda prova 2016 maturità scientifico: i quesiti di matematica articolo

[math]\begin{cases}
& y = k \\
& 1 - ax^2 = k
\end{cases} \hspace{1cm} \begin{cases}
& y = k \\
& 1 - ax^2 = y
\end{cases}[/math]

[math]x \pm \sqrt{\frac{1 - k}{a}}[/math]

base rettangolo =

[math]2 \sqrt{\frac{1-k}{a}}[/math]

altezza rettangolo = k

Area rettangolo =

[math]2k \sqrt{\frac{1-k}{a}}[/math]

Perimetro rettangolo =

[math]4 \sqrt{\frac{1-k}{a}} + 2k[/math]

Massimizziamo l'area:

[math]2 \sqrt{\frac{1-k}{a}} - \frac{2k}{2\sqrt{\frac{1-k}{a}}} = \frac{2 \sqrt{1-k}}{\sqrt{a}} - \frac{k \sqrt{a}}{\sqrt{1 - k}} = \frac{2(1-k)- ak}{\sqrt{a} \sqrt{1-k}} = 0[/math]

[math]2 - 2k - ak = 0[/math]

[math]k (a + 2) = 2][/math]

[math]k = \frac{2}{2+a} \hspace{2cm}[/math]
Sostituisco questo valore di k nel perimetro

Perimetro rettangolo =

[math]4 \sqrt{\frac{1 - \frac{2}{2+a}}{a}} + \frac{4}{2+a} = \frac{4}{\sqrt{2+a}} + \frac{4}{2+a} = \frac{4\sqrt{2+a} + 4}{2+a} = \frac{4(\sqrt{2+a}+1)}{2+a}[/math]

Massimizziamo il perimetro:

[math]\frac{\frac{\not{4}^{2}}{\not{2}\sqrt{2+a}}(2+a)- 4(\sqrt{2+a} + 1)}{(2+a)^2} = \frac{-2\sqrt{2+a} - 4}{(2+a)^2} = 0[/math]

[math]-2\sqrt{2+a} - 4 = 0[/math]

[math]\sqrt{2+a} = -2[/math]

[math]2+a = 4[/math]

[math]a = 2[/math]

Quesito numero 3

Volume sfera =

[math]\pi \int_{a}^{b} [f(x)]^2 dx = \pi \int_{-2}^{+2} (r^2 - x^2) dx = \pi [r^{2}x - \frac{x^3}{3}]_{-2}^{2} = \pi (r^3 - \frac{r^3}{3} + r^3 - \frac{r^3}{3}) = \frac{4}{3} \pi r^3[/math]

[math]\pi \int_{0}^{h-r} (r^2 - x^2) dx = \pi [r^{2}x - \frac{x^3}{3}]_{0}^{h-r} = \pi [r^{2}h - r^3 - \frac{(h-r^3)}{3}][/math]

Sottraendo dal volume totale

[math]\frac{4}{3} \pi r^3[/math]
, il volume di metà sfera
[math]\frac{2}{3} \cdot 4 \pi r^3[/math]
e il volume ricevuto prima, otteniamo:

Volume calotta =

[math]\pi \cdot (2h^2 - \frac{h^3}{3})[/math]

Quesito numero 4

10 domande

4 risposte a domande

1 risposta esatta per ogni domanda

A = "Rispondere almeno a otto domande"

P(A) = ?

P(A) = P(0 errori) + P(1 errore) + P(2 errori)

P (0 errori) =

[math](\frac{1}{4})^{10}[/math]

P (1 errore) =

[math]\binom{n}{1} (\frac{3}{4}) \cdot (\frac{1}{4})^9[/math]

P (2 errori) =

[math]\binom{n}{2} (\frac{3}{4})^2 \cdot (\frac{1}{4})^8[/math]

[math]P(A) = \frac{1}{4}^{10} + 10\cdot \frac{3}{4} \cdot \frac{1}{4}^9 + \binom{10}{2}(\frac{3}{4})^2 \cdot (\frac{1}{4})^8 =[/math]

[math](\frac{1}{4})^8 [(\frac{1}{4})^2 + \frac{15}{2}(\frac{1}{4}) + 45 (\frac{3}{4})^2][/math]

[math]\frac{109}{262144} \cong0,000416[/math]

Quesito numero 5

[math]K (-2, 1, 2) \hspace{2cm} P ?[/math]
punto di tangenza

[math]\pi : 2x - 2y + z - 9 = 0[/math]

Vettore di parametri direttori del piano

[math]\pi[/math]

[math]V = P - K = [x_{p} - x_{k}, \hspace{0,5cm} y_{p} - y_{k}, \hspace{0,5cm} z_{p} - z_{k}][/math]

[math]= [x_{p} + 2,\hspace{0,5cm} y_{p} + 1, \hspace{0,5cm} z_{p} - 2][/math]

Sostituiamo parametri direttori di V in

[math]\pi[/math]
:

[math](x_{p} + 2) \cdot x + (y_{p} + 1) \cdot y + (z_{p} - 2) \cdot z + d = 0[/math]

[math]\left.\begin{matrix}
x_{p} + 2 = 2\\
y_{p} + 1 = -2 \\
z_{p} - 2 = 1
\\
\end{matrix}\right\} \hspace{1cm}[/math]
Per l'equazione data di
[math]\pi[/math]

[math]x_{p} = 0[/math]

[math]y_{p} = -3 \hspace{2cm}[/math]
[math]P(0,-3,3)[/math]
punto tangenza

[math]z_{p} = 3[/math]

[math]\overline{PK}[/math]
= raggio

r =

[math]\sqrt{(x_{p} - x_{k})^2 + (y_{p} - y_{k})^2 + (z_{p} - z_{k})^2}[/math]
=

[math]\sqrt{(0 + 2)^2 + (-3 + 1)^2 + (3 - 2)^2}[/math]
=
[math]\sqrt{4 + 4 + 1} = 3[/math]

Quesito numero 6

[math]\exists P(x) |\hspace{1cm} \left |P(x) - \cos x \right | \leq 10^{-3} \hspace{0,5cm} \forall \hspace{0,2cm} x \hspace{0,2cm} \epsilon \hspace{0,2cm} \mathbb{R}[/math]

Poiché

[math]P(x) = a_{n} x^n + a_{n -1} x^{n-1} + [/math]
...
[math]+ a_{0} \hspace{0,3cm} , \hspace{0,3cm} a_{n}\neq0[/math]

con

[math]a_{n}, \hspace{0,2cm}[/math]
...
[math], \hspace{0,2cm}a_{0} \hspace{0,2cm} \epsilon \hspace{0,2cm} \mathbb{R}[/math]
e
[math]n \geq 1,[/math]
a seconda del segno di
[math]a_{n} \lim_{x \to \infty} P(x) = \pm \infty[/math]

In entrambi i casi

[math]\left |P(x) - \cos x \right |[/math]
non può essere
[math]\leq 10^{-3} \forall \hspace{0,2cm} x \hspace{0,2cm} + \hspace{0,2cm} \mathbb{R} [/math]

Nel caso limite che

[math]P(x) = a_{0} = cost,[/math]

[math]\left |P(x) - \cos x \right | = \left |a_{0} - \cos x \right |[/math]
non può essere
[math]\neq 10^{-3} \forall \hspace{0,2cm} x \hspace{0,2cm} \epsilon \hspace{0,2cm} \mathbb{R} [/math]
oscillando il
[math]\cos x[/math]
tra -1 e 1 periodicamente.

Quesito numero 7

Ci stiamo chiedendo quale è la probabilità che la pedina passi per B (in posizione (3,5)) in uno dei percorsi che vanno da O(0,0) ad A (in posizione (7,7)).
Quindi sarebbe la probabilità di passare in B sapendo che sono andato da O ad A in 14 passi.

Considero i percorsi totali per A in 14 passi
NOTA: Posso arrivare in A solo in 14 passi, perché 7+7=14.

[math]\binom{14}{7} =\frac{14!}{7!7!}[/math]

I percorsi totali per B (in 8 passi perché 3+5=8

[math]\binom{8}{3} =\frac{8!}{3!5!}[/math]

Se sono in B, i percorsi totali da B ad A in 6* passi saranno:

[math]\frac{6!}{4!2!}=15[/math]

*una volta che sono arrivato in B posso considerarla la nuova origine, rispetto alla quale il punto A è in posizione (4,2)

Per determinare tutti i percorsi che arrivano ad A passando per B, quindi, basta fare:

[math]\frac{7!7!}{14!} \frac{8!}{3!5!} 15 \approx 0,245[/math]

Quesito numero 8

[math]f(x): \mathbb{R} \to \mathbb{R}[/math]

[math]f(x) = e^x (2x + x^2)[/math]

Si cerca la primitiva di

[math]f(x)[/math]
passante per
[math](1, 2e)[/math]

[math]g(x) = \int f(x)dx \hspace{2cm} ; \hspace{1cm} g(1) = 2e[/math]

[math]g(x) = \int 2xe^x dx + \int x^2e^xdx[/math]

[math]\int 2xe^x dx = \hspace{1cm} 2xe^x - \int 2e^xdx = \hspace{1cm} 2xe^x - 2e^x[/math]

[math]\int x^2e^x dx = \hspace{1cm} x^2e^x - \int 2xe^x dx = \hspace{1cm} x^2e^x - 2xe^x + 2e^x[/math]

[math]g(x) = ( {\not2xe^x} - \not{2e^x}) + (x^2 e^x - \not{2xe^x} + \not{2e^x}) + C = x^2e^x + C [/math]

[math]g(1) = 2e \to e + C = 2e \to C = e[/math]

[math]g(x) = x^2e^x + e[/math]

Quesito numero 9

[math]r : \begin{cases}
& \text x = t\\
& \text y = 2t \\
& \text z = t
\end{cases}[/math]

[math]S : \begin{cases}
& \text x + y + z - 3 = 0 \\
& \text 2x - y = 0
\end{cases}[/math]

P (1,0,-2)

(1,2,1) vettore direttore di r

Trasformo s dalla forma cartesiana a parametrica:

[math]S : \begin{cases}
& \text x = 3 - y - z \\
& \text 2 (3 - y - z) - y = 0
\end{cases}[/math]

[math]\begin{cases}
& \text x = 3 - y - z \\
& \text 6 - 2y - 2z - y = 0
\end{cases}[/math]

[math]\begin{cases}
& \text x = 3 - y - z \\
& \text 2z = - 3y + 6
\end{cases}[/math]

[math]\begin{cases}
& \text x = 3 - y - z \\
& \text z = 3 - \frac{3}{2}y
\end{cases}[/math]

[math](-\frac{1}{2}, 1, -\frac{3}{2})[/math]
vettore direttore di S

Date due rette con parametri direttori:

[math](l_{1}, m_{1}, n_{1})[/math]
e
[math]((l_{2}, m_{2}, n_{2}) \exists \pi[/math]
che soddisfa le nostre condizioni. Possiamo calcolare l'equazione cartesiana grazie all'annullamento delle determinanti di questa specifica matrice:

[math]
{\mathcal A} = \left(
\begin{array}{cccc}
x- x_{0} & y - y_{0} & z - z_{0} \\
l_{1} & m_{1} & n_{1} \\
l_{2} & m_{2} & n_{2}\\
\end{array}
\right)
[/math]
con
[math]x_{0}, y_{0}, z_{0}[/math]
coordinate del punto P

[math]{\mathcal A} = \left(
\begin{array}{cccc}
x- 1 & y & z + 2\\
1 & 2 & 1 \\
-\frac{1}{2} & 1 & - \frac{3}{2}\\
\end{array}
\right) = {\mathcal -} \left(
\begin{array}{cccc}
y & z + 2 \\
1 & - \frac{3}{2} \\
\end{array}
\right) + 2 \left(
\begin{array}{cccc}
x - 1 & z + 2 \\
-\frac{1}{2} & - \frac{3}{2} \\
\end{array}
\right) {\mathcal -} \left(
\begin{array}{cccc}
x - 1 & y \\
-\frac{1}{2} & 1 \\
\end{array}
\right) = [/math]

[math]= -(-\frac{3}{2}y - z - 2) + 2 (-\frac{3}{2}x + \frac{3}{2} + \frac{1}{2}z + 1) - (x - 1 + \frac{1}{2}y) =[/math]

[math]= \frac{3}{2}y + z + 2 - 3x + 3 + z + 2 - x + 1 - \frac{1}{2}y[/math]

[math]= -4x + y + 2z + 8[/math]

[math]\pi : -4x + y + 2z + 8 = 0[/math]

Quesito numero 10

Data la funzione:

[math]f: ] 1,+\infty \to \mathbb{R})[/math]
tale che
[math]f(x)=\int _{e}^{x^2}{\frac{t}{\ln{t}}dt}[/math]

Per determinare la retta tangente al grafico nel punto

[math]x=\sqrt{e}[/math]
considero:

[math]f’(x)=\frac{x^2}{\ln{x^2}} \cdot 2x[/math]

Quindi:

[math]f’(\sqrt{e})=\frac{e}{ln{e}}\cdot 2\sqrt{e}= 2e\sqrt{e} \hspace{2cm}[/math]
è il coefficiente angolare della retta cercata.

[math]t: y=2e\sqrt{e}x+q[/math]

Per determinare q considero

[math]f(\sqrt{e})=0[/math]
poiché la retta tangente nel punto
[math]x=\sqrt{e}[/math]
ha lo stesso valore della funzione, basta imporre:

[math]2e\sqrt{e} \sqrt{e} +q = 0[/math]
da cui
[math]q = -2e^2[/math]

La retta tangente sarà quindi:

t:

[math]y = 2e\sqrt{e}x -2e^2[/math]

I tutor di Skuola.net sono al lavoro per risolvere questa traccia in modo che gli studenti che terminano la prova possano consultarla. Perciò pubblicheremo la soluzione solo dopo il tempo minimo di consegna dei compiti d'esame (11:30). Consultare le prove d'esame durante lo svolgimento stesso può comportare l'esclusione, perciò consigliamo a tutti i maturandi di non guardare questa pagina mentre sono a scuola.

TEMI MATURITA' 2016: LA HELP LINE

La redazione di Skuola.net sarà a fianco di tutti i maturandi per permettere loro di affrontare con successo le prove della maturità e i temi maturità 2016. Raccoglieremo tutte le vostre segnalazioni e risponderemo alle vostre domande per ognuna delle giornate della maturità 2016, al fine di risolvere ogni dubbio. Le soluzioni dei nostri tutor non saranno tuttavia pubblicate prima dell'orario consentito per legge. Infatti lo scopo è quello di fornire le soluzioni pronte una volta usciti dall'aula d'esame, non quello di far copiare i maturandi e far loro invalidare l'esame di Stato.
Per ogni informazione, dubbio o problema, ecco i nostri recapiti:

via mail a redazione@skuola.net
tramite WhatsApp al numero 3938025594
via Twitter @skuolanet
via Facebook

E allora che aspetti...segui su Skuola.net la Maturità 2016 relativa alla seconda prova di maturità di Matematica, come hai fatto il 22 giugno per la prima prova di Maturità del 2016 di Maturità!

Data pubblicazione 23 Giugno 2016, Ore 12:03

News correlate

Skuola | TV
Play
E ADESSO? La verità su cosa fare dopo la maturità

Rivedi lo speciale di Skuola.net e Gi Group dedicato a tutti i maturandi che vogliono prendere una decisione consapevole sul proprio futuro grazie ai consigli di esperti del settore.

24 giugno 2025 ore 16:00

Segui la diretta