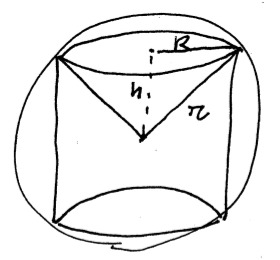
[newpage]Primo quesito
R^2 = r^2 - h^2 \\
V(h) = 2 \pi h (r^2 - h^2) = 2 \pi (r^2 h - h^3) \\
V'(h) = 2 \pi (r^2 - 3 h^2) = 0 \quad \Rightarrow \quad h = \frac{r}{\sqrt{3}} \\
V = 2 \pi \left( r^2 \frac{r}{\sqrt{3}} - \left( \frac{r}{\sqrt{3}} \right)^3 \right)
= 2 \pi \frac{2 r^3}{3 \sqrt{3}} \simeq 522.3742 \ \mathrm{l}
[/math]
Secondo quesito
P \in \text{grafico} \left( \sqrt{x} \right)
\quad \Rightarrow \quad P(x, \sqrt{x}), \quad x \ge 0
\text{Se } A(4,0) \\
\Rightarrow \text{dist}(P,A) = d(x) = \sqrt{(x-4)^2 + (\sqrt{x}-0)^2}
= \sqrt{(x-4)^2 + (\sqrt{x})^2}
= \sqrt{x^2 - 8x + 16 + x}
= \sqrt{x^2 - 7x + 16}
\Rightarrow d'(x) = \frac{1}{2 d(x)} (2x - 7) = 0
\quad \Longleftrightarrow \quad x = \frac{7}{2}
\quad \Rightarrow \quad P\left( \frac{7}{2}, \sqrt{\frac{7}{2}} \right)
[/math]
Terzo quesito
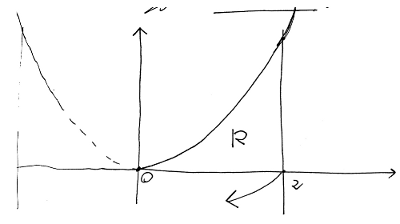
Se
sia
\Rightarrow g(y) = \sqrt[3]{y} \\
x = 0 \Rightarrow y = 0, \quad x = 2 \Rightarrow y = 8 \\
V = V_{\text{cil}} - \pi \int_{0}^{8} \left( \sqrt[3]{y} \right)^2 \, dy
= \pi \cdot 4 \cdot 8 - \pi \left[ \frac{3}{5} y^{\frac{5}{3}} \right]_0^8
= 32 \pi - \frac{3}{5} \pi 8^{\frac{5}{3}}
= 32 \pi - \frac{3}{5} \pi \cdot 32
= \frac{64}{5} \pi[/math]
Quarto quesito
\binom{n}{4} = \binom{n}{3} \\[2mm]
\Rightarrow \frac{n!}{4!(n-4)!} = \frac{n!}{3!(n-3)!} \\[1mm]
n \neq 0 \Rightarrow 4! (n-4)! = 3! (n-3)! \\[1mm]
\Rightarrow 4 \cdot (n-4)! = (n-3) \cdot (n-4)! \quad \text{(poiché $4! = 4\cdot3!$)} \\[1mm]
\Rightarrow 4 = n-3 \Rightarrow n = 7
[/math]
Quinto quesito
A = \int_{1}^{2} |\cos x| \, dx
= \int_{1}^{\frac{\pi}{2}} \cos x \, dx + \int_{\frac{\pi}{2}}^{2} (-\cos x) \, dx \\[1mm]
= \sin x \Big|_{1}^{\frac{\pi}{2}} - \sin x \Big|_{\frac{\pi}{2}}^{2} \\[1mm]
= \big(\sin \frac{\pi}{2} - \sin 1\big) - \big(\sin 2 - \sin \frac{\pi}{2}\big) \\[1mm]
= 1 - \sin 1 - \sin 2 + 1 \\[1mm]
= 2 - \sin 1 - \sin 2
[/math]
Sesto quesito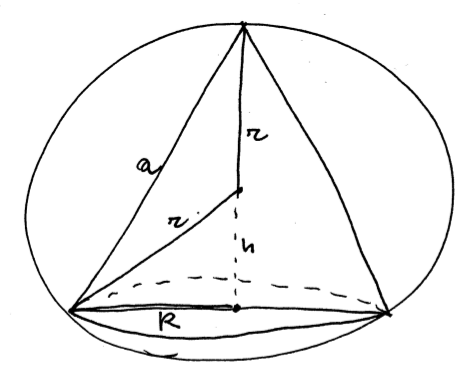 
\lim_{x \to a} \frac{\tan x - \tan a}{x - a}
\stackrel{H}{=} \lim_{x \to a} \frac{1 - \tan^2 x}{1} = 1 + \tan^2 a
[/math]
\text{Pongo } x - a = t \Rightarrow x = t + a \\[1mm]
\lim_{t \to 0} \frac{\tan(t + a) - \tan a}{t}
= \lim_{t \to 0} \frac{1}{t} \left[ \frac{\tan t + \tan a}{1 - \tan t \tan a} - \tan a \right] \\[1mm]
= \lim_{t \to 0} \frac{1}{t} \frac{\tan t + \tan a - \tan a + \tan t \tan^2 a}{1 - \tan t \tan a} \\[1mm]
= \lim_{t \to 0} \frac{\tan t (1 + \tan^2 a)}{1 - \tan t \tan a} \\[1mm]
= \lim_{t \to 0} \frac{\tan t}{t} \cdot \frac{1}{1 - \tan t \tan a} \cdot (1 + \tan^2 a) \\[1mm]
= 1 \cdot 1 \cdot (1 + \tan^2 a) = 1 + \tan^2 a
[/math]
Settimo quesito
f\left(x\right)=x^{2011}+2011x+12=0\\
Dom\left(f\right)=\mathbb{R}\\
lim_{x\rightarrow\pm\infty}f\left(x\right)=\pm\infty\\
f'\left(x\right)=2011x^{2010}+2011\left(x^{2010}+1\right)>0\;\forall x\in Dom\left(f\right)\\
\Rightarrow f[/math]
cresce dappertutto. Poiché
f\left(x\right) f\left(x\right)>0\; x\in[b,+\infty)\\
[/math]
(per il teorema della permanenza del segno)
per il teorema di esistenza degli zeri su
si ha
Poiché poi
Ottavo quesito
il problema della quadratura del cerchio consiste nel costruire con riga e compasso un quadrato equivalente ad un cerchio dato. Il problema, in forma algebrica implica la risoluzione dell'equazione
(l=lato quadrato r=raggio circonferenza) e non ha soluzione a causa della trascendenza di
(la soluzione algebrica è
)
Nono quesito
Se
è un punto di
siano
i vertici del triangolo rettangoo nel piano.
Allora
PA=\sqrt{\left(x-a\right)^{2}+y^{2}+z^{2}}\\
PB=\sqrt{x^{2}+\left(y-b\right)^{2}+z^{2}}\\
PC=\sqrt{x^{2}+y^{2}+z^{2}}\\
[/math]
Ne segue
\begin{cases}
\left(x-a\right)^{2}+y^{2}+z^{2}=x^{2}+y^{2}+z^{2}\\
x^{2}+\left(y-b\right)^{2}+z^{2}=x^{2}+y^{2}+z^2
\end{cases}[/math]
\begin{cases}
x^{2}+a^{2}-2ax=x^{2}\\
y^{2}+b^{2}-2by=y^{2}
\end{cases}
[/math]
da cui
x=\frac{a}{2},\qquad y=\frac{b}{2}
[/math]
e quindi
che è la retta passante per il punto medio dell'ipotenusa AB e perpendicolare al piano che contiene il triangolo
Decimo quesito
I grafici di I e III sono dispari, mentre II è pari. Poiché
g pari
g' dispari
g dispari
g' pari
ciò implica che f deve essere o I o III e f' è II. Poiché f' si annulla in due punti
f ha due punti stazionari e quindi un max e un min. Ne segue che f è la III e la risposta giusta è D
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
