[math]f(x)=\left(ax + b\right) e^{-x/3} + 3[/math]
Impongo
[math]f(0) = 2[/math]
, ottengo
[math]b + 3 = 2 \Rightarrow b = -1[/math]
Calcoliamo la derivata:
[math]f'(x) = -1\frac{1}{3}\left(ax -1\right) e^{-x/3} + a e^{-x/3} = e^{-x/3} \left(- \frac{1}{3}ax + a - \frac{1}{3} \right) \ge 0\\
a x \le 1 + 3a [/math]
a x \le 1 + 3a [/math]
Se voglio avere un massimo, deve essere
[math]a>0[/math]
, e:
[math]x \le \frac{1 + 3a}{a} = 4 \Rightarrow a = 1[/math]
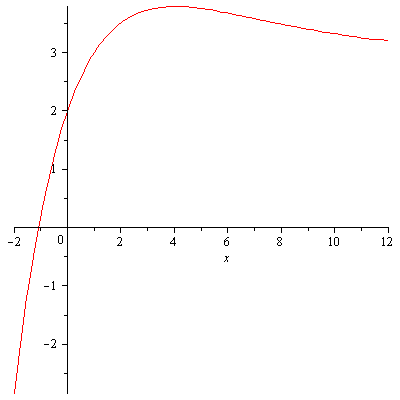
Il grafico è quindi:
La derivata è calcolata, il dominio è tutto l'asse e i limiti sono ovviamente:
[math]\lim_{x\rightarrow +\infty} f(x)=3\\
\lim_{x\rightarrow -\infty} f(x)= -\infty[/math]
\lim_{x\rightarrow -\infty} f(x)= -\infty[/math]
Per la derivata seconda, otteniamo:
[math]f''(x) = e^{-x/3} \left(\frac{1}{9}x - \frac{4}{9} -\frac{1}{3}\right) \ge 0\\
x \ge 7[/math]
x \ge 7[/math]
Abbiamo così trovato il punto di cambio di concavità.
Calcoliamo:
[math]\int_0^3 f(x)dx = \int_0^3 \left(x-1\right) e^{-x^3} dx + 9 =\\= 9 - \left[3 \left(x - 1\right) e^{-x/3}\right]_0^3 + 3 \int_0^3 e^{-x^3} dx =\\
= 9 - 6 e^{-1} - 3 -9 \left[e^{-x^3}\right]_0^3 = 15(1-e^{-1})[/math]
= 9 - 6 e^{-1} - 3 -9 \left[e^{-x^3}\right]_0^3 = 15(1-e^{-1})[/math]
Infine, proviamo che la funzione data verifica i valori forniti:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 3 | 3.51 | 3.73 | 3.79 | 3.76 | 3.68 |
Dallo studio di funzione e dal limite, si ha che già da
[math]x > 1[/math]
si ha
[math]e^{-x/3}\left(x - 1\right) > 0 \Rightarrow f(x) > 3[/math]
, quindi il profitto non può scendere al di sotto di 3 milioni.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
