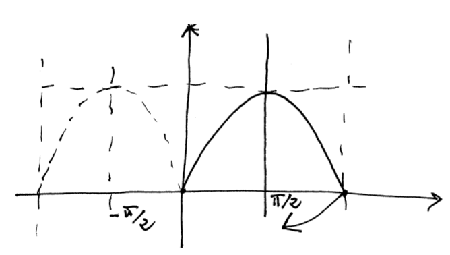
Primo quesitoLa geometria euclidea è l'approssimazione utilizzata correntemente per descrivere il mondo su piccole scale. Aumentando la scala, ad esempio, bisogna considerare la curvatura della superficie terrestre, e per avere una geometria intrinseca abbiamo per forza bisogno di quella non euclidea. Aumentando ancora la scala, intervengono le correzioni della relatività generale, e anche per quelle è indispensabile la geomtria non ecuclidea.
Secondo quesito
Sia
, quindi
.
Se
, la distanza tra P e A è
d(x) = \sqrt{(x - 4)^2 + (\sqrt{x} - 0)^2}
= \sqrt{(x - 4)^2 + x}
= \sqrt{x^2 - 7x + 16}.
[/math]
Per trovare il minimo deriviamo:
d'(x) = \frac{1}{2 d(x)} (2x - 7) = 0
\quad \Longrightarrow \quad x = \frac{7}{2}.
[/math]
Quindi il punto P più vicino ad A è
Terzo quesito
\lim_{x \to a} \frac{\tan x - \tan a}{x - a}
\stackrel{\text{H}}{=}
\lim_{x \to a} 1 - \tan^2 x = 1 + \tan^2 a
[/math]
Poniamo
, allora
:
\lim_{t \to 0} \frac{\tan(t + a) - \tan a}{t}
= \lim_{t \to 0} \frac{1}{t} \left[ \frac{\tan t + \tan a - \tan a + \tan t \tan^2 a}{1 - \tan t \tan a} \right]
[/math]
= \lim_{t \to 0} \frac{\tan t (1 + \tan^2 a)}{1 - \tan a \, \tan t}
= \lim_{t \to 0} \frac{\tan t}{t} \cdot \frac{1 + \tan^2 a}{1 - \tan a \, \tan t}
= 1 + \tan^2 a
[/math]
Quarto quesito
\binom{n}{4} = \binom{n}{3}
\Rightarrow \frac{n!}{4!(n-4)!} = \frac{n!}{3!(n-3)!}
[/math]
,
Quinto quesito
consideriamo la seguente applicazione
\varphi:\mathbb{N}\rightarrow Q^{2}\\
[/math]
dove
Q^{2}=\left\{ n^{2}:n\in\mathbb{N}\right\}\\
[/math]
definita da
\\\varphi\left(n\right)=n^{2}\varphi\left(n\right)=n^{2}
[/math]
tale applicazione è iniettiva e suriettiva
biiettiva. Pertanto possiamo "contare" tutti i quadrati
\begin {array}{c|c|c|c|c|c|c}
\mathbb{N} & 0 & 1 & 2 & 3 & 4 & \ldots \\Q^2 & 0 & 1 & 4 & 9 & 16 & \ldots \end{array}
[/math]
e questo mostra che i quadrati sono tanti quanti i numeri naturali
Sesto quesito
Il massimo si ha per
Settimo quesito
La probabilità di fallire tutte le prove è
, mentre la probabilità di azzeccarne esattamente una è data da
.
Il quesito chiede l'evento complementare a questo, quindi
=1 - \frac{13 \cdot 3^9}{4^10} \simeq 24.4%[/math]
Ottavo quesito
il problema della quadratura del cerchio consiste nel costruire con riga e compasso un quadrato equivalente ad un cerchio dato. Il problema, in forma algebrica implica la risoluzione dell'equazione
(l=lato quadrato r=raggio circonferenza) e non ha soluzione a causa della trascendenza di
(la soluzione algebrica è
)
Nono quesito
Se
è un punto di
siano
i vertici del triangolo rettangoo nel piano.
Allora
PA=\sqrt{\left(x-a\right)^{2}+y^{2}+z^{2}}\\
PB=\sqrt{x^{2}+\left(y-b\right)^{2}+z^{2}}\\
PC=\sqrt{x^{2}+y^{2}+z^{2}}\\
[/math]
Ne segue
\begin{cases}
\left(x-a\right)^{2}+y^{2}+z^{2}=x^{2}+y^{2}+z^{2}\\
x^{2}+\left(y-b\right)^{2}+z^{2}=x^{2}+y^{2}+z^2
\end{cases}[/math]
\begin{cases}
x^{2}+a^{2}-2ax=x^{2}\\
y^{2}+b^{2}-2by=y^{2}
\end{cases}
[/math]
da cui
x=\frac{a}{2},\qquad y=\frac{b}{2}
[/math]
e quindi
che è la retta passante per il punto medio dell'ipotenusa AB e perpendicolare al piano che contiene il triangolo
Decimo quesito
I grafici di I e III sono dispari, mentre II è pari. Poiché
g pari
g' dispari
g dispari
g' pari
ciò implica che f deve essere o I o III e f' è II. Poiché f' si annulla in due punti
f ha due punti stazionari e quindi un max e un min. Ne segue che f è la III e la risposta giusta è D
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
