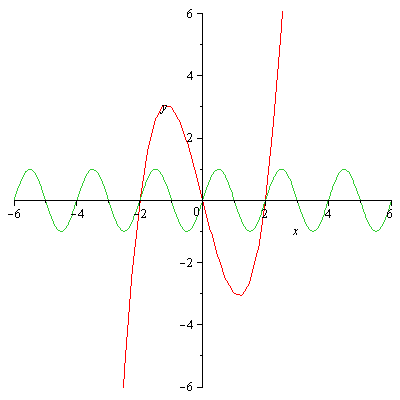
[math]f(x) = x^3 - 4x \\g(x)= \sin(\pi x)[/math]
[math]f(x)[/math]
dominio : [math]\forall x \in \mathbb{R}[/math]
[math] f(-x) = -x^3 + 4x = - (x^3 - 4x) = -f(x)[/math]
dispariint. assi: asse y:
[math] x = 0 \\ f(x) = 0[/math]
Asse x:
[math] y = 0 \\ x(x^2 - 4) = 0 \to x=0\\ x \pm 2 [/math]
positività:
[math]x^3 - 4x > 0 \\x(x-4)>0[/math]
[math]-2>x>0 \cup x>2[/math]
Comportamento all'infinito:
[math]lim_{x \to + \infty} x^3 - 4x = lim_{x\to \infty} x^3 (1- \no{\frac{4}{x^2}}^0) = +\infty[/math]
E siccome dispari:
[math] lim_{x \to \infty} \\f(x) = -\infty[/math]
Andamento:
[math] f'(x) = - 3x^2 - 4 = 0 \\f'(x) = 0 \to 3x^2 - 4 = 0 \to x^2 = \frac{4}{9} \to = x \pm \frac{2 \sqrt3}{3}[/math]
[math]f'(x) = 0 \\3x^2 -4 > 0 \to x > -\frac{2 \sqrt 3}{3} \cup x > \frac {2 \sqrt3}{3}[/math]
Cresce per
[math] x > \frac{ -2 \sqrt3}{3}[/math]
In
[math] x= \frac{-2\sqrt3}{3}[/math]
PUNTO DI MASSIMO RELATIVO
[math] f(\frac{-2\sqrt3}{3}) = (\frac{-2\sqrt3}{3})^3 - 4 (\frac{-2\sqrt3}{3}) = \frac {+16\sqrt3}{9}[/math]
In
[math] x = \frac {+2\sqrt3}{3}[/math]
MINIMO RELATIVO
[math] f(\frac{2\sqrt3}{3}) = \frac {-16\sqrt3}{9})[/math]
[math] f''(x) = 6x \\f''(x) = 0 \to x = 0 [/math]
In
[math] x= 0[/math]
Flesso a tangente obliquaAsintoti obliqui
[math]lim_{x \to \infty} \to \frac{f(x)}{x} = lim_{x\to \infty} \to \frac {x(x^2-4)}{x} = +\infty[/math]
No asintoti obliqui
[math] g(x) = \sin \pi x[/math]
Dominio =
[math]\forall x \in \mathbb{R}[/math]
Int.
assi
[math] x = 0 \\y = 0[/math]
[math] y = 0 \to \sin\pi x = 0 => \sin \pi x = \sin (0 + k \pi) \\ \pi x = 0 + k \pi \\ x = k[/math]
Positività:
[math] \sin \pi x > 0 [/math]
[math] 2k \pi > \pi x > \pi + 2k \pi [/math]
[math] 2k > x > 1 + 2k[/math]
Crescenza/Decrescenza
[math] g'(x) = \pi \cos \pi x [/math]
[math] g' (x) = 0 \to \pi \cos \pi x = 0 => \cos \pi x = 0 \\ \cos \pi x = \cos \frac{\pi}{2} + k \pi [/math]
[math] \pi x = \frac{\pi}{2}+ k \pi \to x = \frac{1}{2} + k[/math]
[math] g'(x) = 0[/math]
[math] \pi \cos \pi x > 0 \\ \cos \pi x > 0[/math]
[math] \cos ( - \frac{\pi}{2} + 2k \pi) > \cos \pi x > ( \frac{ \pi}{2} + 2k \pi})[/math]
[math] - \frac{ \pi}{2} + 2k\pi > \pi x > \frac {\pi}{2} + 2k\pi[/math]
[math] x = \frac{1}{2} + 2k[/math]
Massimi assoluti
[math] g(x) = \sin \pi (\frac12 + 2k \pi) = \sin \frac {\pi}{2} + 2k \pi = 1[/math]
[math] x = - \frac12 + 2k [/math]
Minimi assoluti[math] \sin \pi (- \frac12 + 2k \pi) = -1[/math]
[math] g''(x) = -\pi \sin \pi x \to g''(x) = 0 \\ \pi x = k \pi \\ x = k[/math]
[math] g'' (x) = 0 => - \sin \pi x > 0 \to \sin \pi x > 0 \\ \sin ( - \pi + 2k \pi) > \sin \pi x > \sin (2 k \pi) \\ -1 + 2k > x > 2k[/math]
2)
[math] y = -3 \\ x^3 - 4x = - 3 \\ x^3 - 4x + 3 = 0 \\ f(1) = 1 - 4 + 3 = 0 [/math]
[math]\begin{array} {c|ccc|c}
& 1 & 0 & - 4 & 3 \\
&&&& \\
1 & & 1 & 1 & -3 \\
\hline \\
& 1 & 1 & -3 & 0
\end{array} [/math]
[math] (x - 1) ( x^2 + x -3) = 0[/math]
[math] x = 1[/math]
[math] x^2 + x - 3 = 0 \to x = \frac {- 1 \sqrt{ 1 + 12}}{2} = \frac {-1 \pm \sqrt 13}{2}[/math]
[math] A = (1,3) \\ B \( \frac{1 + \sqrt13}{2}; -3\) \\ C\( \frac {1 - \sqrt13}{2}; -3\)[/math]
[math] Gg : \to g'(x) = \pi \cos \pi x = 0[/math]
[math] \(\frac{1}{2} + 2k, 1\) \ \ per \ \ -3 > k > 2[/math]
[math] \(-\frac{1}{2} + 2k, - 1\) \ \ per \ \ -2 > k > 3[/math]
3)
[math]\int_{0}^{2} g(x) + \int_{2}^{0} f(x) = \\ | - \frac{1}{\pi} \cos \pi x|_0^2 + |\frac{1}{4}x^4 - 2x^2|_2^0 = \\ 0 - (\frac{1}{\no{4}} \cdot \no{16}^4 - 8 ) = + 4[/math]
4) per evitare dubbi di segno, calcoliamo il volume della piscina, dividendone la superficie.
[math] V= V_1 + V_2 - V_3 [/math]
[math] V_1 = \int_0^1 \sin \pi x \cdot h(x) dx [/math]
[math] V_2 = \int_0^2 (4x - x^3) \cdot h(x) dx [/math]
[math] V_3 = \int_1^2 - \sin x \cdot h(x) dx [/math]
e dunque
[math] V_{TOT} = V_1 + V_2 - V_3 = \int_0^1 \sin \pi x \cdot h(x) + \int_0^2 (4x-x^3) \cdot h(x) + \int_1^2 \sin \pi x \cdot h(x) dx [/math]
Unendo
[math] \int_0^1 \sin \pi x \cdot h(x) + \int_1^2 \sin \pi x \cdot h(x) dx = \int_0^2 \sin \pi x \cdot h(x) d(x) [/math]
avremo
[math] V_{TOT} = \int_0^2 (\sin \pi x + 4x - x^3)(3-x) dx [/math]
[math] = \int_0^2 (3-x) \sin \pi x dx + \int_0^2 (12x - 4x^2-3x^3+x^4) dx [/math]
[math] = \[ - \frac{1}{\pi}(3-x) \cos \pi x \]_0^2 - \frac{1}{\pi} \int_0^2 \cos ( \pi x) dx + \[6x^2- \frac43 x^3 - \frac34x^4+ \frac{x^5}{5} \]_0^2 [/math]
siccome
[math] \int_0^2 \cos (\pi x )dx = 0 [/math]
Allora
[math] - \frac{1}{\pi} + \frac{3}{\pi} +24 - \frac{32}{3} - 12 + \frac{32}{5} = \frac{2}{\pi} + \frac{116}{15} [/math]
Il volume in m^3 sara'
[math] ( \frac{2}{\pi} + \frac{116}{15} \) m^3 [/math]
e siccome [math] 1 m^3 = 1000 l [/math]
allora i litri d'acqua saranno [math] \( \frac{2}{\pi} + \frac{116}{15} \) \cdot 10^3 l [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
