Anteprima
Vedrai una selezione di 1 pagina su 2
Disdici quando
vuoi
vuoi
Acquista con carta
o PayPal
o PayPal
Scarica i documenti
tutte le volte che vuoi
tutte le volte che vuoi
Sintesi
PROBLEMA 1 1)
L'area cercata e' differenza tra l'area del settore circolare e quella del triangolo ABO
L'area del settore circolare, dal momento che l'area del cerchio e'
[math] \pi r^2 [/math]
inteso [math] \pi [/math]
la meta' dell'angolo giro, si ricava, ad esempio, attraverso la proporzione[math] \pi r^2: \pi= A: \frac{x}{2} [/math]
da cui
[math] A= \frac{xr^2}{2}[/math]
Del triangolo si sa che tale poligono e' isoscele (due lati sono r).
Per trovare l'area ci occorre la lunghezza del segmento AB e la relativa altezza.
Il segmento AB e' dato, per il teorema di Carnot, da:
[math]AB^2= r^2+r^2-2r^2 \cdot \cos x [/math]
da cui
[math]AB^2=2r^2 \cdot (1-\cos x) [/math]
L'altezza del triangolo sara', per il teorema di Pitagora, utilizzando il triangolo rettangolo meta' del triangolo isoscele
con base pari a metà di AB
[math] OC= \sqrt{r^2- \frac{r^2}{2} + \frac{r^2}{2} \cos x}=[/math]
[math] = \sqrt{ \frac{r^2}{2}(1+ \cos x)}= \frac{r}{ \sqrt{2}} \sqrt{1+ \cos x} [/math]
l'area del triangolo, quindi sara'
[math] A_{AOB}= \frac{1}{2} \cdot \frac{r}{ \sqrt{2}} \sqrt{1+ \cos x} \cdot \frac{2r}{ \sqrt{2}} \sqrt{1- \cos x}= [/math]
[math] = \frac{r^2}{2} \sqrt{1-cos^2} [/math]
che per la relazione fondamentale della trigonometria dara'
[math] \frac{r^2}{2} \cdot \sqrt{ \sin^2 x} [/math]
Trattandosi di un triangolo, x sara' senz'altro compresa tra
[math]0 [/math]
e [math] \pi [/math]
e pertanto la semplificazione di radice non necessitera' del valore assoluto[math] A_{AOB}= \frac{r^2}{2} \sin x [/math]
Pertanto l'area S compresa tra l'arco e la corda sara'
[math]S(x)= \frac{r^2x}{2}- \frac{r^2}{2} \sin x = \frac{r^2}{2} (x- \sin x)[/math]
(Altro modo per risolvere l'area del triangolo poteva essere, piu' semplicemente, valutare l'altezza relativa ad un lato del triangolo pari al raggio;
L'altezza relativa a tale lato, era, per la definizione di seno, data da:
[math] r \sin x [/math]
dal momento che il seno, per definizione, è il rapporto tra il cateto non adiacente l'angolo x e l'ipotenusa e quindi
[math] \frac{h}{r}= \sin x [/math]
)2)
Studio della funzione
Intersezione con gli assi
[math] S(0)=0 [/math]
Dal momento che la funzione
[math] \sin x<x \forall x \in \mathbb{R}^+ [/math]
non esisteranno altri punti di intersezione con l'asse x.Segno della funzione
[math] S(x)>0 \forall \ x \in D [/math]
La funzione e' limitata e definita su tutto il dominio, pertanto non esistono limiti.
Studio della derivata prima:
[math] S'(x)= \frac{1}{2}(1- \cos x) \ge 0 [/math]
[math]\cos x \ne 1 \ \forall x \in D [/math]
Pertanto
[math]S(x)[/math]
e' sempre crescenteDal momento che la funzione è ristretta ed e' sempre crescente, in
[math]x=0[/math]
avremo un minimo assoluto di coordinate [math](0,0)[/math]
e in [math]2 \pi [/math]
un punto di massimo assoluto [math]( 2 \pi, \pi) [/math]
Studio della derivata seconda
[math]S''(x)= \frac{ \sin x}{2} \ge 0[/math]
Da cui
[math]\sin x \ge 0 [/math]
e pertanto
[math] 0 \le x \le \pi \ U \ x=2 \pi [/math]
Concluderemo quindi che nell'intervallo
[math](0, \pi) [/math]
la funzione avrà concavita verso l'alto, nell'intervallo [math]( \pi, 2 \pi) [/math]
verso il basso e nei punti [math] 0 \ \pi \ \ 2 \pi[/math]
punti di flesso.
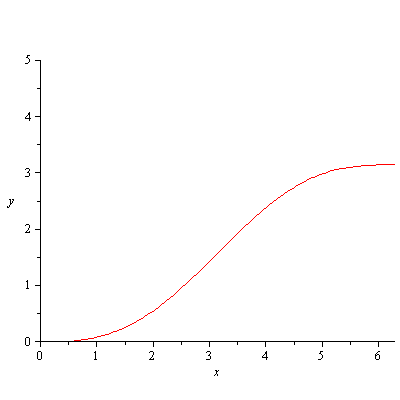
3)
Uguagliata l'area del settore circolare trovata (cfr punto 1) a
[math]100 m^2 [/math]
[math] A_{AOB}= \frac{1}{2}xr^2= 100 m^2 [/math]
si ricava
[math]x= \frac{200}{r^2}[/math]
Posto l l'arco di circonferenza AB ne calcoliamo la lunghezza in funzione di r(anche questo, ad esempio, tramite una proporzione)
[math] 2 \pi r: 2 \pi = l :x [/math]
Da cui
[math]l=xr[/math]
[math]P(r)= 2r + xr= 2r + \frac{200}{r}=2 (r+ \frac{100}{r})[/math]
Attraverso lo studio della derivata prima
[math]P'(r)=2(1- \frac{100}{r^2})[/math]
Otteniamo
[math]2(1- \frac{100}{r^2}) \ge 0[/math]
[math]\frac{r^2-100}{r^2} \ge 0[/math]
Il denominatore, sempre positivo, non partecipa allo studio del segno della frazione.
Posto pertanto
[math]r\ne 0 [/math]
[math]r^2-100 \ge 0[/math]
[math]r^2-100 \ge 0 [/math]
[math]r \le -10 \ U \ r \ge 10[/math]
[math]r \le -10 [/math]
non ha significato, trattandosi della lunghezza del raggio della circonferenza, pertanto l'unico intervallo sara' [math] r \ge 10 [/math]
La funzione sara' decrescente nell'intervallo
[math](0, 10)[/math]
crescente in [math]r > 10 [/math]
e pertanto avra' minimo per [math]r=10[/math]
[math]P(10)=40 [/math]
[math]x= \frac{200}{r^2}=2 [/math]
che e' l'ampiezza dell'angolo espressa in radianti.L'angolo
[math] \alpha [/math]
espresso in gradi, sara' dato da[math] \alpha : 360^{ \circ}=x:2 \pi[/math]
[math] \alpha= \frac{360^{\circ}}{ \pi} \approx 114,59^{\circ}[/math]
4)
[math]r=2 \ \ x= \frac{ \pi}{3}[/math]
[math]0 \le x \le 2[/math]
dal momento che al più x potrà coincidere con il raggio.Disegnata la situazione in un opportuno sistema di assi cartesiani, posto il raggio OB sull'asse delle ascisse e O sull'origine, il punto P avrà coordinate
[math]P(\alpha,0)[/math]
OA sarà la retta di pendenza
[math] \tan \frac{ \pi}{3}[/math]
e pertanto tutti i punti ad essa appartente (dal momento che passa per l'origine..) avranno coordinate[math] ( \alpha, \sqrt{3} \alpha) [/math]
Il lato del quadrato, sarà pertanto
[math] \sqrt{3} \alpha [/math]
quando [math]\alpha\le 1[/math]
, mentre per [math]1\le \alpha\le 2[/math]
tale punto apparterrà all'arco di circonferenza di equazione [math]x^2+y^2=4[/math]
e avrà coordinate [math](\alpha,\sqrt{4-\alpha^2})[/math]
.Il calcolo del volume del solido di rotazione sarà
[math] W= \int_0^2{l^2( \alpha)d \alpha}[/math]
[math]= \int_0^1{3 \alpha^2 d \alpha}+\int_1^2 (4-\alpha^2)\ d\alpha[/math]
[math]= [ \alpha^3]_0^1+[4\alpha-\alpha^3/3]_1^2=1+8-8/3-4+1/3=8/3[/math]
PROBLEMA 2
1)
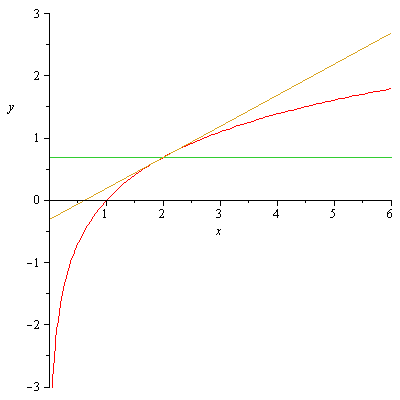
Ogni punto appartentente alla funzione ha coordinate generiche
[math](\alpha, \log \alpha)[/math]
L'equazione della retta generica, passante per un punto
[math] (x_0,y_0) [/math]
e tangente ad una funzione [math]f(x)[/math]
ha equazione generica[math]y-y_0=f'(x)(x-x_0)[/math]
e pertanto, per quanto detto sopra, la retta t del caso avra' equazione
[math] y- \log \alpha= f'(x)(x- \alpha)[/math]
[math]t_P: \ y= \frac{1}{\alpha}x - 1 + \log \alpha [/math]
Il punto A, di ascissa nulla, avra' coordinate
[math](0, \log \alpha - 1) [/math]
E il punto B, avra' anch'esso ascissa nulla e ordinata a quella del punto P generico.
[math](0, \log \alpha)[/math]
Il segmento AB, segmento a cui appartengono due punti aventi stessa ascissa, avrà lunghezza pari alla differenza delle ordinate (in valore assoluto) ovvero
[math]AB=| \log \alpha - \log \alpha +1|=1 [/math]
E dunque il segmento AB sara' costante e uguale a 1.
Per la seconda parte, si procede in maniera analoga.
La retta t si ricava dalla relazione
[math]y- \log_a \alpha = \frac{1}{ \alpha \log a}(x- \alpha)[/math]
E pertanto
[math]y= \frac{x}{\alpha \log a}- \frac{1}{ \log a}+ \log a [/math]
E i punti A e B avranno rispettivamente coordinate generiche
[math]A(0, \log_a \alpha - \frac{1}{ \log a}) [/math]
[math]B(0, \log_a \alpha)[/math]
Da cui, la distanza AB sara'
[math] AB= \frac{1}{ \log a} [/math]
, che varia a seconda del valore di a.2)
Il punto di ascissa 1 ha ordinata 0.
La pendenza del del piano
[math]\delta [/math]
sarà data sia dalla derivata prima della funzione nel punto in esame che dalla tangente dell'angolo.Pertanto
[math] \tan 45^\circ = g'(1) [/math]
Ovvero
[math] 1= \frac{1}{\log a} [/math]
Che risolta, darà
[math]\log a= 1 [/math]
[math] a= e^1 = e [/math]
Nel caso di
[math] \delta = 135 \circle [/math]
avremo[math]-1= \frac{1}{\log a} [/math]
Da cui
[math] a = \frac{1}{e} [/math]
3)
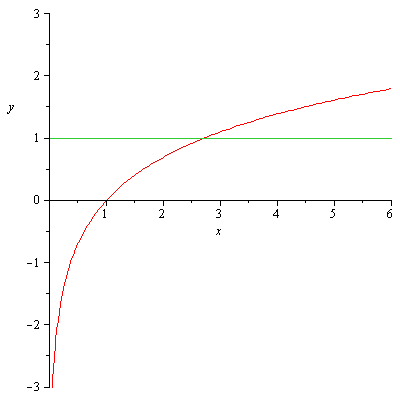
Detto Q il punto di intersezione tra la funzione e la retta y=1,Q' la proiezione di Q sull'asse delle ascisse, R e O i punti di intersezione tra l'asse y e rispettivamente le rette y=1 e y=0, l'Area D richiesta dal problema sarà data dall'area del rettangolo RQQ'O - l'area sottesa dalla funzione.
Sapendo che le coordinate dei punti sono
[math]Q(e,1) [/math]
e [math] Q(e,0)[/math]
L'area del rettangolo sara' data da
[math] e [/math]
mentre l'area della regione sara'[math] \int_1^e \log x \ dx [/math]
integrando per parti
[math] [x \cdot \log x|_1^e - \int_1^e dx] [/math]
E pertanto l'area di D sara'
[math] e - e +0 + e -1 = e-1 [/math]
4)
[math]y= \log x [/math]
da cui [math]x=e^y[/math]
Il centro di rotazione e' sull'asse x=-1 (lavorando sulla funzione inversa) pertanto trasliamo di +1 per avere asse di rotazione x=0.
Otteniamo cosi' la funzione
[math]h(y)=e^y+1[/math]
[math]V_D= \pi \int_0^1 h(y)^2 \ dy - V_{cil} [/math]
dove
[math]V_{cil}[/math]
è il volume del cilindro di raggio=1 e altezza = 1.[math]V_D= \pi \int_0^1(e^y+1)^2 \ dy - \pi = [/math]
[math]\pi [ \int_0^1(e^{2y}+2e^y+1) \ dy - 1] [/math]
[math]\pi [ \frac{1}{2}e^{2y} |_0^1 + 2e^y |_0^1 + y |_0^1 - 1 ]= [/math]
[math]\pi [ \frac{1}{2}e^2- \frac{1}{2}+2e-2+1-1]= [/math]
[math]\pi[ \frac{e^2}{2}+2e- \frac{5}{2}] [/math]
QUESTIONARIO
1)
[math]f'(x)= \sin x [/math]
[math] \int f'(x)dx= F(x)[/math]
[math] F(x)= \int \sin x dx = - \cos x +c [/math]
[math] F(0)=2 [/math]
[math] - \cos(0) + c = 2 [/math]
[math]-1+c=2 [/math]
[math]c=3[/math]
[math]F(x)=3 - \cos x [/math]
2)
Dal momento che l'immagine coincide con il codominio (ovvero ogni elemento "y" dell'insieme B)e ogni elemento è immagine di almeno un elemento di A (dominio) esistono funzioni suriettive.
L'assenza di un numero sufficiente di elementi nell'insieme B rende impossibile la presenza di un'immagine distinta per ogni elemento del Dominio.
non esiste pertanto alcuna funzione iniettiva.
Dal momento che, per definizione, una funzione è bijettiva se è sia suriettiva che iniettiva (deve esistere corrispondenza biunivoca tra gli elementi del dominio e del codominio) non esisteranno nemmeno funzioni bijettive.
3)
E' data
[math]y=x^3+kx^2+3x-4[/math]
I punti a tangente orizzontale sono quelli per cui la derivata prima si annulla.
la derivata prima e'
[math]y'=3x^2+2kx+3[/math]
Che si annulla in
[math]3x^2+2kx+3=0[/math]
Affinche' le soluzioni dell'equazione di secondo grado siano una sola, il Delta della soluzione dovra' essere nullo.
[math]\Delta=4k^2-36=0[/math]
4)
L'affermazione è falsa: non esiste nessun poliedro regolare le cui facce sono esagoni. La spiegazione è questa: consideriamo uno qualsiasi dei vertici di un poliedro regolare. Se cerchiamo di sviluppare (= stendere su un piano) tutte le facce che insistono su quel vertice, otteniamo dei poligoni regolari con un vertice in comune. La somma degli angoli piani che insistono su quel vertice deve essere per forza strettamente minore di 360°, perché altrimenti non sarebbe possibile "piegare" i poligoni e costruire una figura solida.
Cerchiamo di fare questo con degli esagoni regolari (che hanno angoli ai vertici di 120°). Poiché un angolo solido ha almeno 3 facce, servono minimo 3 esagoni, ottenendo un angolo totale di esattamente 360°. Poiché non si riusciamo ad ottenere un angolo minore di 360°, non è possibile ottenere un poliedro regolare.
5)
E' possibile solo alla prima, e il risultato è 0.
La motivazione è questa:
[math]\frac{a}{b} = c[/math]
per definizione vuol dire che [math]c \cdot b = a[/math]
Nel primo caso, dire
[math]\frac{0}{1} = x[/math]
vuol dire [math]x \cdot 1 = 0[/math]
. Questo può succedere solo se x = 0 (dato che 0 è elemento neutro dell'addizione e di conseguenza elemento nullificatore del prodotto)Nel secondo caso, dire
[math]\frac{0}{0} = x[/math]
vuol dire [math]x \cdot 0 = 1[/math]
. Ma poiché 0 è nullificatore, il risultato della moltiplicazione è 0 indipendentemente dal valore di x. x quindi è indeterminato, può assumere qualsiasi valore, e quindi non ha un valore numerico univoco.Nel terzo caso, dire
[math]\frac{1}{0} = x[/math]
vuol dire [math]x \cdot 0 = 1[/math]
. Ma poiché 0 è nullificatore, il risultato della moltiplicazione è per forza 0, e quindi l'equazione è impossibile (si usa in senso improprio per sottointendere un passaggio al limite).Nel quarto caso, per i teoremi sulle potenze
[math]0^0 = 0^{a-a} = \frac{0^a}{0^a} = \frac{0}{0}[/math]
e si rimanda al secondo caso.6)
[math] \lim_{x \to - \infty} \frac{sqrt{x^2+1}}{x} [/math]
[math] \lim_{x \to - \infty} \frac{sqrt{x^2(1+ \frac{1}{x^2})}}{x} [/math]
Dal momento che
[math]\frac{1}{x^2} \to 0 [/math]
avremo[math] \lim_{x \to - \infty} \frac{sqrt{x^2}}{x} [/math]
Dal momento che la semplificazione della radice (al numeratore) porterebbe all'utilizzo del valore assoluto, consideriamo che il limite e' a -infinito e pertanto il valore assoluto cambia il segno di x.
[math] \lim_{x \to - \infty} \frac{-x}{x} [/math]
Semplificano Numeratore e Denominatore otteniamo
-1
7)
[math]\left(\begin{array}{c} n \\ k+1\end{array}\right)=[/math]
[math]\frac{n!}{(k+1)!(n-(k+1))!}[/math]
[math]\frac{n!}{(k+1)!(n-k-1)!}[/math]
Dal momento che
[math](k+1)!=(k+1)k![/math]
e che
[math](n-k-1)!= \frac{(n-k)(n-k-1)!}{n-k}= \frac{(n-k)!}{n-k} [/math]
Possiamo riscrivere
[math]\frac{n!}{(k+1)!(n-k-1)!}[/math]
come
[math]\frac{n!}{(k+1)k!} \cdot \frac{n-k}{(n-k)!}[/math]
Scambiando l'ordine dei fattori al numeratore e al denominatore, otteniamo
[math] \frac{n-k}{k+1} \cdot \frac{n!}{k!(n-k)!}[/math]
e, sapendo che
[math] \frac{n!}{k!(n-k)!}= \left(\begin{array}{c} n \\ k\end{array}\right) [/math]
dimostriamo l'uguaglianza
8 )
Si provi che l'equazione
[math]x^{2009} + 2009 x + 1[/math]
ha una sola radice compresa fra -1 e 0
Soluzione: scriviamo
[math]f(x) = x^{2009} + 2009 x + 1[/math]
[math]f'(x) = 2009x^{2008} + 2009[/math]
Studiamo il segno della derivata:
[math]2009x^{2008} + 2009 > 0[/math]
[math]x^{2008} > -1[/math]
Siccome una potenza pari è sempre non negativa, la derivata è sempre positiva e la funzione è sempre crescente. Quindi può avere l'equazione può avere al massimo una soluzione (essendo crescente, la funzione è negativa prima della radice e positiva dopo).
Dimostriamo che la soluzione esiste ed è compresa tra -1 e 0
[math]f(-1) = (-1)^{2009} + 2009 \cdot (-1) + 1 = -1 -2009 + 1 = -2009[/math]
[math]f(0) = 0^{2009} + 2009 \cdot 0 + 1 = 1[/math]
Per il teorema dei valori intermedi delle funzioni continue (e un polinomio è ovviamente continuo), la funzione tra -1 e 0 assume tutti i valori tra -2009 e 1, quindi assumerà anche il valore 0.
Conclusione: la soluzione esiste, è unica ed è compresa tra -1 e 0
9)
Il teorema di Cavalieri enuncia che se due solidi hanno tutte le sezioni congruenti allora hanno stesso volume.
si tagli il cilindro con un piano parallelo alla base.
Il piano interseca cono e scodella..
Le due figure che otteniamo, sono un cerchio (tra piano e cono) ed una corona circolare (tra piano e scodella)
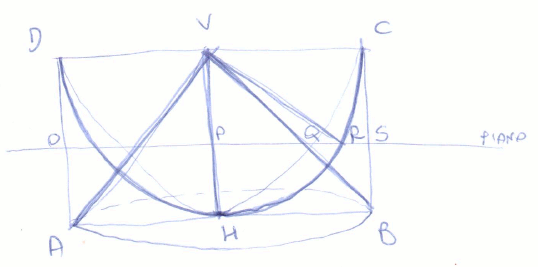
VHB e rettangolo in H
l'angolo VPQ=90°, dal momento che i triangoli HBV e PQV sono simili (condividono l'angolo in V e hanno l'angolo VQP e VBH corrispondenti (Talete))
Posto VP=h, l'area del cerchio sarà
[math]S= \pi h^2 [/math]
L'area del settore circolare sarà invece:
per il teorema di Pitagora
[math]PR= \sqrt{VR^2-PV^2}= \sqrt{r^2-h^2} [/math]
Area della scodella sarà
[math] \pi (PS^2-PR^2) = \pi (r^2-(r^2-h^2))= \pi h^2 [/math]
Che dimostra che le aree sono, appunto, uguali.
10)
Posto
[math] f(x)= \cos 5x [/math]
Sapendo che il periodo di
[math] \cos \alpha [/math]
e' [math]2 \pi [/math]
detto T il periodo che dobbiamo trovare, poniamo
[math] \cos (5(x + T)) = \cos 5x [/math]
da cui
[math] \cos (5x+5t)= \cos 5x [/math]
posto
[math] 5x= \alpha [/math]
(dove [math]\cos \alpha [/math]
ha periodo [math] 2 \pi [/math]
)[math] 5x+5t=5x+2 \pi [/math]
pertanto
[math] t= \frac{2 \pi}{5} [/math]
Estratto del documento
Pag. 1/2 Sessione ordinaria 2009
Seconda prova scritta
M557 – ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
SCIENTIFICO
Indirizzo:
MATEMATICA
Tema di:
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.
PROBLEMA 1
È assegnato il settore circolare di raggio e ampiezza ( e sono misurati, rispettivamente, in
r x r x
AOB
e ).
metri radianti
1. Si provi che l’area compresa fra l’arco e la corda è espressa, in
S AB
1 [ ]
( ) ( ) π
= − ∈
2 sen con .
funzione di , da 0
, 2
x S x r x x x
2
( )
2. Si studi come varia e se ne disegni il grafico (avendo posto
S x
= 1 ).
r 2
Si fissi l’area del settore pari a 100 m . Si trovi il valore di per
3. r
AOB
il quale è minimo il perimetro di e si esprima il corrispondente
AOB
valore di in gradi sessagesimali (è sufficiente l’approssimazione al
x
grado). π
=
4. Sia = 2 e . Il settore AOB è la base di un solido le cui sezioni ottenute con piani ortogonali
r x W
3
ad sono tutte quadrati. Si calcoli il volume di
OB W.
PROBLEMA 2
Nel piano riferito a coordinate cartesiane, ortogonali e monometriche, si tracci il grafico della funzione
G
f
( ) = (logaritmo
log naturale)
f x x
Sia il punto d'intersezione con l’asse della tangente a in un suo punto Sia il punto
1. A y G P. B
f
d’intersezione con l’asse della parallela per all’asse . Si dimostri che, qualsiasi sia il
y P P,
x della funzione
segmento ha lunghezza costante. Vale la stessa proprietà per il grafico
AB G
g
( ) = log con reale positivo diverso da 1?
g x x a
a
Sia δ l’inclinazione sull’asse della retta tangente a nel suo punto di ascissa 1. Per quale valore
2. G
x g
è δ = 45°? E per quale valore di è δ = 135°?
della base a a
3. Sia la regione del primo quadrante delimitata dagli assi coordinati, da e dalla retta d’equazione
G
D f
= 1 . Si calcoli l’area di .
y D
Si calcoli il volume del solido generato da nella rotazione completa attorno alla retta d’equazione
4. D
= − .
1
x
Dettagli
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
