Matematica...mente

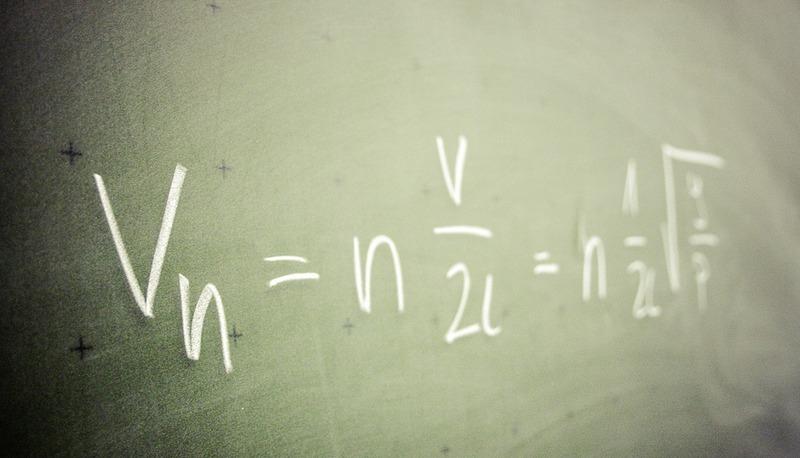
E ancora ritroviamo riferimenti in Edgar Allan Poe, in Kafka, Calvino e

Buzzati.

Esempi poi tipici di come, soprattutto nella letteratura più recente si è

cercato di muoversi sempre più in direzione della matematica, sono

Flatland di Edwin Abbott, che descrive dettagliatamente la geometria di

Sphereland

un mondo piatto piano (il cosiddetto «planiverso»), di Dionys

I racconti scientifici

Burger, che descrive un mondo piatto ma sferico, di

Charles Hinton, che sperimentano invece un mondo quadridimensionale

Centomila miliardi di poemi

e di Raymond Queneau, basati sul calcolo

combinatorio.

LA COMMEDIA & I NUMERI

La Divina Commedia ha una complessa simbologia numerica: a partire

dalla struttura, che si divide in 3 cantiche(il tre è il numero perfetto, della

Trinità) composte ciascuna di 33 Canti (33 corrisponde all’età di Cristo

alla sua morte e alla sua risurrezione), a cui si aggiunge il I Canto

dell’Inferno che funge da prologo (e che rende il totale dei Canti uguale a

100, 10X10, quando 10 è il numero dei comandamenti), si nota infatti la

costante presenza dei cosiddetti numeri sacri o magici, il tre, che

connota la struttura(anche i Canti sono divisi in terzine), il suo multiplo

nove, che è il numero delle gerarchie angeliche, dei cerchi infernali e

delle zone del Purgatorio, il sette (forse perchè sette sono le virtù

cardinali e teologali sette i peccati capitali?).

Tantissimi sono poi i riferimenti numerologici in Dante, riguardanti

molteplici branche della matematica, dalla geometria

O cara piota mia, che sì t'insusi,

che come veggion le terreni menti

non capere in triangol due ottusi… Paradiso, XVII 13 - 15:

8

(che si riferisce al fatto che in un triangolo non possono esserci due

angoli ottusi)

Qual è ‘l geomètra che tutto tal era io a quella vista nova;

s’affigge veder volea come si convenne

per misurar lo cerchio, e non l’imago al cerchio e come vi

ritrova, s’indova

pensando, quel principio ond’elli

indige,

(il chiaro riferimento è qui all’annosa questione della quadratura del

cerchio)

alla probabilità,

Quando si parte il gioco della zara,

colui che perde sì riman dolente

repetendo le volte, e tristo impara… Purgatorio, VI, 1-3

Interessante è poi la questione del XXXIIIsimo Canto del Purgatorio, nel

‘nel quale un cinquecento diece e cinque

quale la frase ’ ha fatto

discutere.

Scrivendo infatti il numero con la notazione romana, si ottiene DXV,

ritenuto da molti un anagramma. Potrebbe infatti riferirsi a DUX, Arrigo

VII, al monogramma greco di Cristo, o ancora a Domini Xristi Vergatus, la

misteriosa figura del Veltro che ha lasciato molti dibattiti aperti, o a

Domini Xristi Vicarius, il Papa.

Facendo invece riferimento alla notazione araba, anche se non si ha la

sicurezza che Dante la conoscesse già, il DXV potrebbe diventare 515,

che i numerologi indicano come distanza tra Terra e Cielo, espressa in

anni, facendo riferimento ad Ezechiele, o ancora, considerando la lingua

greca, 515 ha come codificazione Parthenos, “Vergine”, mentre

considerando il latino 515 diventerebbe ‘Mather Christi’…coincidenza?

Ma esaminiamo degli esempi più concreti…

L’incendio suo seguiva ogni

scintilla;

ed eran tante, che ‘l numero

loro

più che ‘l doppiar delli scacchi

s’immilla.

Ci troviamo nel XXVIII canto del

Paradiso, in cui Dante tratta la 9

questione della funzione degli Spiriti Angelici e della loro eventuale

presenza, che è stata fulcro di molti dibattiti dei teologi medioevali.

Gli ordini angelici appaiono come nove cerchi di fuoco concentrici che

ruotano con una velocità che è proporzionalmente inversa alla loro

distanza dal centro, punto luminoso che rappresenta Dio.

I versi si riferiscono in particolare al numero degli angeli, argomento

affrontato anche in molti passi della Bibbia e dallo stesso Dante nel

Convivio, numero che l’autore ritiene particolarmente significativo, tanto

da utilizzare un paragone che lo mette a confronto con una cifra che,

data la sua enormità, è quasi impensabile.

Dante si rifà alla leggenda di Sissa Nasir, inventore degli scacchi

decapitato perché il sovrano a cui propose la sua invenzione si sentì

preso in giro dalla ricompensa richiestagli, che apparentemente

sembrava invece essere molto modesta.

Il furbo Nasir, mostrandogli la scacchiera 8 X 8 gli richiese infatti un

chicco di grano per la prima casella, due per la seconda, quattro per la

terza, otto per la quarta e così via fino alla 64esima, l’ultima.

Per comprendere meglio l’entità della cifra che ne sarebbe derivata si

ricorre spesso a un espediente, immaginare cioè di distribuire i chicchi di

Nasir sulla superficie terrestre, che oggi sappiamo pari a

cm2:

5,0995X10alla18 dato che i chicchi risulterebbero 18 446 744 073

709 551 615 otterremmo 3 chicchi e mezzo per ogni cm2 della superficie

terrestre; il numero a cui Dante accenna è però ancora più grande,

perché ‘più che raddoppiare di casella in casella’, ‘s’inmilla’, e con lo

stesso calcolo fatto precedentemente avremmo un numero immenso, 10

alla 189, di angeli per ogni cm2!

Ma come si ottiene un numero così elevato?

PROGRESSIONI GEOMETRICHE

Una progressione geometrica è una successione di numeri tali che il

quoziente tra due elementi consecutivi è sempre uguale a un numero

ragione

costante, detto della successione.

Un esempio può essere il seguente:

4; 8; 16; 32 ...

8/4 = 2

16/8 = 2

32/16 = 2

... 10

Il quoziente costante, che nell'esempio è 2, si chiama ragione della

progressione geometrica e si indica con q.

Il termine n-esimo di una progressione può quindi essere definito così:

a = a · q

n n-1

Il termine n-esimo di una progressione geometrica, noto il primo termine

e la ragione è:

a = a · q^

n 1 (n-1)

Quindi in una progressione geometrica:

se q > 0 i termini sono tutti o positivi o negativi

se q < 0 i termini sono alternativamente positivi e negativi.

Il termine di posto s di una progressione geometrica, noto il termine di

posto r e la ragione è:

as= ar · q^(s-r)

Il prodotto di due termini equidistanti dagli estremi di una progressione

geometrica è costante ed è uguale al prodotto dei termini estremi.

La somma dei primi n termini di una progressione geometrica di ragione

q è:

Sn =a (q^ – 1)

n

1 q-1

Il prodotto dei primi n termini di una progressione geometrica di

ragione q è uguale alla radice del prodotto del primo e dell’ultimo

termine, elevata all’indice di quest’ultimo. 11

E ancora… Come quando dall'acqua o da uno

Come quando da l'acqua o da lo specchio un raggio rimbalza verso

specchio la parte opposta, risalendo allo stesso

salta lo raggio a l'opposita parte, modo

saltando su per lo modo parecchio di com'era disceso, e si allontana

a quel che scende, e tanto si dalla perpendicolare per un tratto

diparte uguale, così come dimostrano

dal cader de la pietra in igual l'esperienza e la scienza;

tratta,

sì come mostra esperienza e arte; così mi sembrò di essere colpito da

una luce riflessa proprio davanti a

così mi parve da luce rifratta me; per cui la mia vista fu pronta a

quivi dinanzi a me esser percosso; sfuggirne.

per che a fuggir la mia vista fu

ratta. Purgatorio, XV

E sì come secondo raggio suole E come il raggio riflesso è determinato

uscir dal primo e risalire in suso, solitamente dal raggio incidente, e ritorna

pur come pelegrin che tornar alla sorgente come un pellegrino che

vuole, voglia tornare [come un falco pellegrino

che risale dopo essere piombato sulla

preda],

così de l'atto suo, per li occhi così da questo gesto di Beatrice,

infuso entrato nella mia facoltà immaginativa

ne l'imagine mia, il mio si fece, attraverso gli occhi, derivò il mio

e fissi li occhi al sole oltre sguardo e fissai gli occhi nel Sole in

nostr'uso. modo non consentito alle capacità

umane. Paradiso, I

In entrambi questi passaggi, che appartengono rispettivamente al XV

Canto del Purgatorio e al I del Paradiso, Dante accenna al fenomeno della

riflessione, uno dei più caratteristici effetti della luce.

Nel primo, Dante procede verso Ovest scortato da Virgilio, finchè una

luce abbagliante lo investe, impedendogli la vista e costringendolo a

voltarsi: la luce proviene dall’angelo della mansuetudine, che li accoglie

per condurli al girone superiore; nel secondo passo, Dante e Beatrice

sono in volo verso il Cielo della Luna, e Dante è stupito dal fatto che gli è

possibile fissare il Sole, cosa non normalmente consentita alle facoltà

umane.

E’ particolare, soprattutto nelle terzine del Purgatorio, l’attenzione

particolare che Dante ha nel descrivere minuziosamente il fenomeno, e

la più comune interpretazione attribuita a tale atteggiamento è il voler

evidenziare l’estrema armonia della natura, che attraverso la

particolarità delle sue leggi e dei suoi comportamenti ci mostra la

presenza di Dio.

RIFLESSIONE E RIFRAZIONE Francesco Maria Grimaldi,

De Lumine

La luce, emessa da sorgenti primarie, sole, lampadina, fiamma, si

propaga attraverso mezzi trasparenti e anche attraverso il vuoto. I

fenomeni quali riflessione, rifrazione etc si hanno quando le onde

luminose incontrano un ostacolo, o più in generale una discontinuità, e la

luce non viaggia così indisturbata dalla sorgente in poi.

Nella riflessione speculare, che avviene

quando la luce incide su superfici lucide, ad

ogni raggio incidente che colpisce la

suddetta superficie, corrisponde un solo

raggio riflesso. Chiamando angolo di

incidenza l'angolo formato dal raggio e la

normale alla superficie e angolo di riflessione

quello formato dalla normale e dal raggio

riflesso, si ottiene che l'angolo di riflessione è uguale all'angolo di

incidenza e che il raggio riflesso, quello incidente e la normale staranno

nello stesso piano.

Quando un raggio luminoso passa da un

materiale ad un altro la radiazione cambia

direzione di propagazione: questo fenomeno

si chiama rifrazione. L'entità della deviazione

dipende dalla differenza di indice di

rifrazione tra i due materiali.

Proprio questa deviazione è la ragione per

cui quando guardiamo in acqua vediamo gli

oggetti spostati rispetto alla loro posizione

reale e le aste sembrano spezzate. L'indice

di rifrazione di un materiale dipende alla

lunghezza d'onda della radiazione, e questo provoca il fenomeno della

dispersione.

…Non esiste cosa alcuna che l'arte non possa

esprimere… Oscar Wilde

Sono innegabili i rapporti che intercorrono fra matematica e arte, tanto

che la stessa matematica è stata più volte definita essa stessa una forma

d’arte, l’arte dei numeri.

Anche riferendosi alle arti figurative e all’architettura è inevitabile

imbattersi in legami con la matematica, da cui l’architettura non può

prescindere e che è presente spesso, anche se forse più velatamente, in

molte opere pittoriche.

A iniziare dalla prospettiva, che è la rappresentazione realistica di scene

spaziali su un piano, e che è stata ampiamente utilizzata da Brunelleschi

e da Piero della Francesca, dopo la teorizzazione di Leon Battista Alberti,

e continuando con Leonardo(di cui è celebre anche il motto “proibita la

lettura ai non matematici”, ripreso forse da Platone), il primo ad

introdurre, attorno al 1500, le anamorfosi, rappresentazioni che appaiono

corrette soltanto se osservate da un punto di vista particolare, che

ispirarono la geometria proiettiva, lo studio delle proprietà che sono

invarianti rispetto a proiezione(che si sviluppò in una delle branche

fondamentali della matematica), la matematica ha quindi costituito da

sempre un elemento importante per l’arte.

Ma oltre gli artisti più antichi, come Paolo Uccello, che venne addirittura

«accusato» dal Vasari di essere più un matematico che un artista, o

Albrecht Dürer, che scrisse un libro sulle figure piane e solide, e produsse

l'incisione Melanconia, in cui compaiono strani solidi ed un quadrato

magico, notiamo affinità con la matematica anche analizzando le

avanguardie del ‘900. Wassily Kandinsky, che fondò con Franz Marc

la corrente Der blaue reiter, (“Il cavaliere

azzurro”), può aiutarci a capire meglio il valore

ed il significato della matematica nell’arte, in

quanto teorizzò nell’opera ‘Lo spirituale

nell'arte’, la sostituzione dell'immaginazione