.jpg)
Per affrontare al meglio la prova di matematica del 2015 è bene muoversi con anticipo. Cominciare ad esercitarsi già da ora, quindi, è un'ottima strategia per arrivare pronti all'esame di maturità del liceo scientifico. Può essere utile, a tal proposito, rivedere il calcolo di un'area sottesa ad una curva, uno degli argomenti più ostici che uno studente del liceo scientifico deve affrontare. Con l'aiuto del prof di matematica, Francesco Bologna, vedremo come risolvere questo problema sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.
Scopri tutte le tracce della maturità scientifica degli anni passati
Impara ad usare la calcolatrice, guarda il nostro video!
CALCOLO DI UN'AREA SOTTESA AD UNA CURVA
Uno degli esercizi più impegnativi che deve affrontare uno studente liceale è il calcolo di aree sottese a curve di cui si conosce l'equazione. Senza entrare in tecnicismi, ricordiamo che, dal teorema fondamentale del calcolo integrale possiamo ricavare la formula per il calcolo di dell'area espressa dalla relazione di Newton - Leibniz:
\[\int_a^bf\left(x\right)dx=F\left(b\right)-F(a)\]
Dove
è una qualsiasi primitiva di
ed
e
sono gli estremi di integrazione.
Per determinare tale integrale definito dobbiamo, innanzitutto, ricordare il significato di primitiva di una funzione:
Si dice che
Due primitive differiscono a meno di una costante.
Risalire alla primitiva di una funzione non è sempre banale.
Diverse sono le tecniche che vengono studiate quali ad esempio l'integrazione per sostituzione e l'integrazione per parti; tecniche non sempre di immediata applicazione.
CALCOLO DI UN'AREA SOTTESA AD UNA CURVA
Esempio: determinare l'area sottesa alla curva di equazione
Nell'intervallo
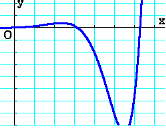
Iniziamo con il determinare la primitiva della funzione.
Per far ciò dovremo utilizzare la formula di integrazione per parti:
\[
\int{f}\left(x\right)\bullet{}h^{'}\left(x\right)\ \
dx=f\left(x\right)\bullet{}h\left(x\right)-\int{f^{'}}\left(x\right)\bullet{}h\left(x\right)\
dx\]
Scegliamo come
la funzione
e come
Sapendo che:
\[
\int{e^xdx=e^x+c}
\]
Si ha che
. Determinato
si ha:
\begin{equation}
\int{e^xsen}(x)\ \ dx=e^x\ sen(x)\ -\int{e}^x\ cos(x)dx\ \ \ \ \ \ \ \ \ (1)
%eq1
\end{equation}
A questo punto possiamo osservare che il secondo integrale non è immediatamente risolvibile.
Siamo quindi costretti a riapplicare la formula di integrazione per parti anche per questo secondo integrale otterremo:
\begin{equation}
\int{e^x}cos\left(x\right)\ dx=e^xcos(x)\ -\int-e^x\ sen(x)dx\ \ \ \ \ \ \ \ \ \
\ (2)
%eq2
\end{equation}
Sostituendo la (2) nella (1) si avrà:
\[
\int{e}^xsen\left(x\right)\ dx=e^x\
sen\left(x\right)-e^xcos\left(x\right)-\int{e}^xsen\left(x\right)\ dx
\]
Infine si avrà:
\[
\int{e}^xsen\left(x\right)\ dx={(e}^x\
sen\left(x\right)-e^xcos\left(x\right))\bullet{}\frac{1}{2}+c
\]
A questo punto possiamo applicare la relazione di Leibniz:
\[
\int_a^bf\left(x\right)dx=F\left(b\right)-F(a)
\]
Sostituendo prima b e poi a al posto della
si otterrà il valore dell'area pari a 278,750.
Vediamo come la calcolatrice FX991ES+ può rendere la procedura banale.
Passaggio #1
Attraverso al combinazione:
Selezioniamo la modalità RAD.
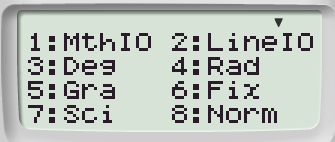
Passaggio #2
Utilizziamo il comando di integrazione definita presente a sinistra del tasto cursore:

Dopo aver trascritto la funzione utilizzando la funzione ALPHA.

Digita =.
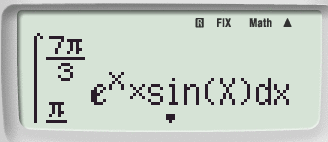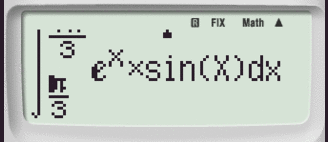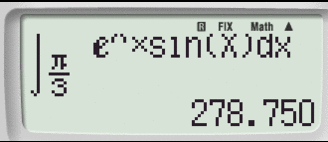






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo