Trigonometria: Se alpha è l'angolo indicato in figura, calcolare: ....

Se

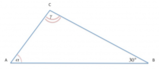
è l'angolo indicato in figura, calcolare:

a)

;

b)

Svolgimento

Sappiamo che, essendo per definizione la cotangente di un angolo l'ascissa del punto di intersezione fra la retta tangente la circonferenza nel punto

e la retta passante per l'estremo dell'arco, sappiamo che:

Ricaviamo quindi la tangente dell'angolo:

Troviamo ora il seno e il coseno dell'angolo, sapendo che, poiché esso si trova nel secondo quadrante, il primo sarà positivo, mentre il secondo negativo:

Svolgimento (a)

Per risolvere tale quesito, abbiamo bisogno del coseno dell'angolo

e della sua tangente; poiché abbiamo già questi valori, possiamo procedere alla sostituzione:

Svolgimento (b)

In questo caso abbiamo bisogno del seno dell'angolo

e della sua secante; abbiamo tutti i dati necessari per poter ricavare questi valori.

Troviamo quindi la secante dell'angolo: