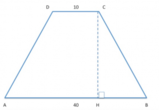
Trigonometria problemi: Nel trapezio ABCD , avente base maggiore AB , si sa che: AD = 3a , DC = a sin(alpha) = sin(hat{BAD}) = 4/5 , cos(γ) = cos(hat{BCD}) = - frac(5)(13) ....

Nel trapezio

, avente base maggiore

, si sa che:

Determinare:

1. le altre funzioni goniometriche di α e γ e le funzioni goniometriche di
   [math]δ =hat{ADC}[/math]
   e
   [math] β = hat{ABC}[/math]
   ;
2. l'altezza
   [math]CH[/math]
   relativa ad
   [math]AB[/math]
   , il lato obliquo
   [math]CB[/math]
   e la base maggiore
   [math]AB[/math]
   ;
3. le funzioni goniometriche di
   [math]hat{ABD}[/math]
   ;
4. le funzioni goniometriche di
   [math]hat{DBC}[/math]
   .

Svolgimento (1)

Determiniamo le altre funzioni goniometriche di α e γ mediante la relazione fondamentale:

Per trovare le funzioni goniometriche degli angoli δ e β

teniamo presente che il trapezio è un quadrilatero avente gli angoli adiacenti supplementari. Possiamo quindi scrivere che:

Calcoliamo ora le loro funzioni goniometriche:

Considerando gli angoli associati abbiamo che:

Svolgimento (2)

Per determinare l'altezza

, consideriamo il triangolo rettangolo

, considerando che

; applichiamo il primo teorema dei triangoli rettangoli:

Determiniamo il lato obliquo

considerando il triangolo

:

Con il teorema di Pitagora, troviamo il lato

:

Sappiamo che il segmento

è uguale alla base minore e misura quindi

;

Determiniamo ora il lato

del triangolo

:

Possiamo ora trovare la lunghezza della base maggiore:

Svolgimento (3)

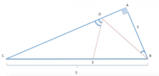
Per trovare le funzioni goniometriche di

consideriamo il triangolo

.

Possiamo trovare il lato

con il teorema del coseno:

Applicando ora il teorema del seno, possiamo ricavare il seno dell'angolo

:

d) Troviamo ora le funzioni goniometriche dell'angolo

sapendo che:

Applichiamo la formula di sottrazione del coseno: