Trigonometria problemi: Dato il trapezio isoscele ABCD avente: AB = 40 , CD = 10 , tg(hat{ABC}) = 4/3 ....

di _francesca.ricci

Ominide

2 min. di lettura

Vota

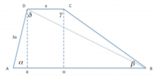
Dato il trapezio isoscele

[math]ABCD[/math]

avente:

[math] AB = 40 , CD = 10 , tg(hat{ABC}) = 4/3 [/math]

determinare:

perimetro e area del trapezio;
dopo aver dimostrato che il trapezio è circoscritti bile ad una circonferenza, i raggi
[math]R[/math]
e
[math]r[/math]
delle circonferenze inscritta e circoscritta.

Svolgimento (1)

Per prima cosa, troviamo la lunghezza del segmento

[math]HB[/math]

[math] HB = frac(AB - DC)(2) = frac(40 - 10)(2) = 15 [/math]

Consideriamo il triangolo rettangolo

[math]CHB[/math]

. Possiamo determinare il valore del cateto

[math]CH[/math]

utilizzando il secondo teorema dei triangoli rettangoli:

[math]CH = HB \cdot tg(hat{ABC}) = 15 \cdot 4/3 = 20 [/math]

Possiamo quindi calcolare l'area del trapezio

[math] A_(ABCD) = frac(AB + DC)(2) \cdot CH = frac(40 + 10)(2) \cdot 20 = 25 \cdot 20 = 500 [/math]

Ora troviamo il lato obliquo

[math]BC[/math]

con il teorema di Pitagora:

[math]CB = \sqrt{CH^2 + HB^2} = \sqrt(20^2 + 15^2) = \sqrt(400 + 225) = \sqrt(625) = 25 [/math]

Calcoliamo il perimetro:

[math]P_(ABCD) = AB + DC + CB + DA = 40 + 10 + 25 + 25 = 100 [/math]

Svolgimento (2)

Ricordiamo che un quadrilatero è inscrivibile in una circonferenza se la somma di due angoli apposti è uguale agli altri due; poiché il trapezio in questione è isoscele, è sicuramente inscrivibile.

Un quadrilatero è circoscrivibile quando la somma di due lati opposti è uguale a quella degli altri due:

[math]AB + DC = AD + CB [/math]

[math] 40 + 10 = 25 + 25 \to 50 = 50 [/math]

Il trapezio è quindi inscrittibile in una circonferenza:

Notiamo che il diametro della circonferenza inscritta è uguale all'altezza del trapezio:

[math]CH = 2r \to 20 = 2r \to r = 10 [/math]

Essendo

[math]AH = DC + HB = 10 + 15 = 25 [/math]

, possiamo determinare la lunghezza del cateto

[math]AC[/math]

del triangolo rettangolo

[math]ACH[/math]

[math]AC = \sqrt{CH^2 + HA^2} = \sqrt(20^2 + 25^2) = \sqrt(400 + 625) = \sqrt(1025) = 5 \sqrt(41) [/math]

Possiamo poi utilizzare il teorema della corda per risalire al valore del diametro della circonferenza circoscritta:

[math] AC = D \cdot \\sin (hat{ABC})[/math]

Possiamo poi ricavare il seno dell'angolo

[math]hat{ABC}[/math]

dalla sua tangente:

[math]\\sin (hat{ABC}) = frac(tg(hat{ABC}))(\sqrt{1 + tg^2 (hat{ABC})}) = frac(4/3)(\sqrt(1 + (4/3)^2)) = [/math]

[math] frac(4/3)(\sqrt{1 + frac(16)(9)}) = frac(4/3)(\sqrt(frac(25)(9))) = frac(4/3)(5/3) = 4/3 \cdot 3/5 = 4/5 [/math]

[math] D = frac(AC)(\\sin (hat{ABC})) = frac(5 \sqrt{41})(4/5) = 5 \sqrt{41} \cdot 5/4 = frac(25 \sqrt{41})(4) [/math]

[math] R = D/2 = frac(25 \sqrt{41})(4) \cdot 1/2 = frac(25 \sqrt{41})(8) [/math]

Trigonometria problemi: Dato il trapezio isoscele ABCD avente: AB = 40 , CD = 10 , tg(hat{ABC}) = 4/3 ....

Esercizio di trigonometria: trapezio isoscele inscrittibile in una circonferenza, applicazione delle regole trigonometriche

Svolgimento (1)

Svolgimento (2)

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Svolgimento (1)

Svolgimento (2)

Appunti correlati

Trigonometria problemi: Nel trapezio ABCD , avente base maggiore AB , si sa che: AD = 3a , DC = a sin(alpha) = sin(hat{BAD}) = 4/5 , cos(Î³) = cos(hat{BCD}) = - frac(5)(13) ....

Trigonometria problemi: La diagonale AC del quadrilatero ABCD lo divide nel triangolo equilatero ABC di lato l e nel triangolo isoscele ACD di lato AC = CD = l . Sapendo che cos(hat{BCD}) = - frac(1)(sqrt3) , calcolare l'area del quadril

Trigonometria problemi: Nel triangolo ABC rettangolo in A si sa che AB = 3 e BC = 5 . Siano D un punto di AC tale che tg(hat{ABD}) = 2/3 ed E il punto di BC tale che risulti hat{EDC} = 2 hat{ABD} .

Trigonometria problemi: Il un triangolo due lati AB e BC misurano rispettivamente 2° e 3° ed è cos(hat{ABC}) = - 1/5 . Detta H la proiezione di C sulla retta AB , calcolare il perimetro del triangolo AHC.

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.