Trigonometria problemi: Il un triangolo due lati AB e BC misurano rispettivamente 2° e 3° ed è cos(hat{ABC}) = - 1/5 . Detta H la proiezione di C sulla retta AB , calcolare il perimetro del triangolo AHC.

Problema di trigonometria: calcolare il perimetro di un triangolo, applicazione delle regole trigonometriche

_francesca.ricci
di _francesca.ricci
Ominide
2 min. di lettura
Vota

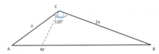
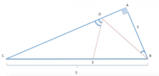
Il un triangolo due lati

[math]AB[/math]

e

[math]BC[/math]

misurano rispettivamente

[math]2°[/math]

e

[math]3°[/math]

ed è

[math] \\cos(hat{ABC}) = - 1/5 [/math]

.

Detta

[math]H[/math]

la proiezione di

[math]C[/math]

sulla retta

[math]AB[/math]

, calcolare il perimetro del triangolo

[math]AHC[/math]

.

Svolgimento

Ricaviamo il lato

[math]AC[/math]

del triangolo

[math]ABC[/math]

mediante il teorema del coseno:

[math] AC^2 = AB^2 + BC^2 - 2 \cdot AB \cdot BC \cdot \\cos(hat{ABC})[/math]

[math] AC^2 = (2a)^2 + (3a)^2 - 2 \cdot 2a \cdot 3a \cdot (- 1/5) = 4a^2 + 9a^2 + (12)/5 a^2 = (77)/5 a^2[/math]

Quindi:

[math] AC = \sqrt{ (77)/5 a^2 } = \sqrt((77)/5) a [/math]

Consideriamo ora il triangolo rettangolo

[math]CHB[/math]

: possiamo trovare il valore del cateto

[math]CH[/math]

mediante il primo teorema sui triangoli rettangoli:

[math] CH = BC \cdot \\sin (hat{ABC}) [/math]

Ricaviamo quindi

[math]\\sin (hat{ABC}) [/math]

dalla relazione fondamentale:

[math] \\sin (hat{ABC}) =\sqrt{1 - \\cos^2 (hat{ABC})} = \sqrt(1 - (- 1/5)^2) = [/math]

[math] \sqrt{1 - 1/(25)} = \sqrt(frac(24)(25)) = frac(2 \sqrt6)(5) [/math]

[math] CH = BC \cdot \\sin (hat{ABC}) = 3a \cdot frac(2 \sqrt6){5} = frac(6 \sqrt6){5} a [/math]

Il triangolo

[math]AHC[/math]

è rettangolo, poiché uno dei suoi cateti è costituito dal segmento

[math]CH[/math]

, cioè l'altezza del triangolo

[math]ABC[/math]

relativa al lato

[math]AB[/math]

.

Avendo le lunghezze dei lati

[math]AC[/math]

e

[math]CH[/math]

, possiamo trovare con il teorema di Pitagora il cateto

[math]AH[/math]

:

[math] AH = \sqrt{CA^2 - CH^2} = \sqrt((\sqrt((77)/5) a)^2 - (frac(6 \sqrt6)(5) a)^2 ) = [/math]

[math] \sqrt{ frac(77)(5) a^2 - frac(216)(25) a^2} = \sqrt(frac(385 - 216)(25) a^2) =[/math]

[math] \sqrt{frac(169)(25) a^2} = frac(13)(5) a[/math]

Possiamo ora determinare il perimetro del triangolo

[math]AHC[/math]

:

[math] P_(AHC) = AH + HC + CA = frac(13)(5) a + frac(6 \sqrt6){5} a + frac(\sqrt(77))(\sqrt5) a = [/math]

[math] frac(13\sqrt5 a + 6 \sqrt{30} a + 5 \sqrt(77) a)(5\sqrt5)[/math]

Razionalizziamo:

[math] frac(13\sqrt5 a + 6 \sqrt{30} a + 5 \sqrt(77) a)(5\sqrt5) \cdot frac(\sqrt5)(\sqrt5) = [/math]

[math] frac((13\sqrt5 a + 6 \sqrt{30} a + 5 \sqrt(77) a) \cdot \sqrt5)(5\sqrt5 \cdot \sqrt5) = [/math]

[math] frac(65a + 6 \sqrt{150} a + 5 \sqrt(385) a)(25) = frac(65a + 30 \sqrt(6) a + 5 \sqrt(385) a)(25) [/math]

Mettiamo in evidenza 5 e semplifichiamo:

[math] frac(5 ( 13a + 6 \sqrt{6} a + \sqrt(385) a))(25) = frac(13a + 6 \sqrt{6} a + \sqrt(385) a)(5) [/math]

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Help (321322)
filo.22 di filo.22

Aiuto urgente per compiti
anitaminardi1987 di anitaminardi1987

Problema con potenze
gagix12 di gagix12

I migliori insegnanti di Matematica

Giovanni

Giovanni C.

Supertutor
Percorsi
Verificato

Insegnante di Aiuto tesi, Contabilità e bilancio, Controllo di gestione, Diritto

a partire da 20 €/ora
most booked
Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Mostra altri Tutor