Metodo Montecarlo e ottimizzazione: investimenti in obbligazioni

Tra i principali, e più efficaci, metodi di ottimizzazione numerica di una funzione libera o vincolata vi sono il metodo del simplesso, il metodo GRG, i metodi evolutivi degli algoritmi genetici. Anche Excel adotta questi tre algoritmi



Io ho di me stesso l'immagine di un uomo,
il quale dopo aver cozzato in molti scogli,
ed evitato a malapena il naufragio passando in una secca,
conservi ancora la temerarietà di mettersi per mare
con lo stesso battello sconquassato,
con l'intatta ambizione di tentare il giro del mondo
nonostante queste disastrose circostanze.
David Hume.

Tutti i modelli sono sbagliati, ma alcuni sono utili.
George Box

Introduzione alla Ottimizzazione

Alcuni dei principali, e più efficaci, metodi di ottimizzazione (massimo o minimo) numerica di una funzione libera o vincolata sono: il metodo del simplesso, il metodo GRG (Generalized Reduced Gradient), i metodi evolutivi (in particolare gli algoritmi genetici). Anche Excel adotta questi tre algoritmi (integrati dal Branch and bound se si tratta di problemi a variabili intere o miste).

In generale ci si riferisce a problemi del tipo:

Max o min di Y = f(Xi) (i = 1,…n) soggetta a:

1. li <= Xi <= Li Bounds, cioè limiti inferiori (li) e superiori (Li) delle variabili;


2. Vk = vk (Xi) >=< 0 (k = 1,…m; i = 1,….n).

Se la funzione obiettivo "f" ed i vincoli "vk" sono lineari il problema si dice di programmazione lineare e può essere risolto adottando il metodo del Simplesso di Dantzig . Simplesso significa poliedro convesso. Nel piano sono poliedri convessi i rettangoli, i parallelogrammi, i poligoni regolari e irregolari cioè quelli che hanno la proprietà che, comunque scelti al loro interno due punti, il segmento che li congiunge appartenga al poligono stesso. Nello spazio tridimensionale esempi di poliedri convessi sono i cubi, i parallelepidi, i prismi, i solidi platonici, ecc. Dantzig ha scoperto che, se un problema è di programmazione lineare, la soluzione ottimale si trova tra uno dei vertici del poliedro (salvo casi particolari in cu si può trovare su uno spigolo o una faccia del poliedro). Inoltre l'algoritmo del Simplesso permette di evolvere, grazie solo a valutazioni locali, da un vertice del poliedro ad un altro che migliora la funzione obiettivo.

Il metodo GRG (Generalized Reduced Gradient) è stato originariamente ideato da Carpentier ed Abadie, mentre lavorava alla Eletricité de France. Il metodo prevede il calcolo delle derivate parziali della funzione obiettivo rispetto a tutte le variabili Xi per procedere poi, sempre sulla base di valutazioni locali nella direzione di massima ascesa (in caso di ricerca del massimo) o di massima discesa (nel caso di ricerca del minimo). GRG ha tre grossi limiti:

1. l'algoritmo può restare intrappolato in un ottimo locale;


2. non riesce a considerare i punti di frontiera della regione ammissibile;


3. non riesce a gestire i punti angolosi e quelli di discontinuità della funzione obiettivo.

I metodi evolutivi (G.Box ed altri) ed in particolare gli algoritmi genetici (J.Holland ed altri) tentano di trasferire alcuni aspetti delle teorie di Darwin dalla biologia alla ottimizzazione matematica. In particolare gli algoritmi genetici si basano su tre punti:

1. la selezione delle soluzioni migliori;


2. l'incrocio dei valori delle variabili tra coppie di soluzioni migliori (crossover);


3. variazioni casuali nel valore di alcune variabili (mutazioni).

Il fatto di non usare le derivate e di avere all'interno dell'algoritmo elementi di casualità permettono agli algoritmi genetici di affrontare problemi di ottimizzazione non lineare con presenza di ottimi locali e discontinuità delle funzioni. Si parla infatti di programmazione "non liscia" (Non Smoothed Programming). I tre metodi sopra sommariamente descritti (Simplesso, GRG, Algoritmi Evolutivi) sono anche i tre metodi che Excel, che si appoggia per la ottimizzazione a Frontlyne Systems , ha adottato per il suo Risolutore, incluso tra gli add-ins del Menù Strumenti.

Una maniera alternativa di affrontare i problemi di ottimizzazione, è quella di utilizzare la potenza crescente dei computer, per esplorare sistematicamente la regione ammissibile del problema. Questa strategia, basata sulla forza bruta dei moderni sistemi di calcolo, è sicuramente poco efficace. Un po' più efficiente risulta la strategia Montecarlo consistente nell'esplorare casualmente la regione ammissibile memorizzando sempre il miglior risultato trovato. Ovviamente anche il metodo Montecarlo, non avendo alcun algoritmo di convergenza sulla soluzione migliore, non può che considerarsi un metodo per la ricerca di una soluzione soddisfacente (approssimata all'ottimo), ma non un metodo per cercare l'ottimo assoluto di una funzione.

Caso 0: Una funzione plurimodale, non liscia.

Per esemplificare quanto scritto sopra consideriamo una semplice funzione monodimensionale del tipo Y = f(X) per valutare il comportamento dei vari approcci alla ottimizzazione su un caso estremamente semplice.

Funzione obiettivo da ottimizzare Y(X):






Con (1 le X le 25) e:

a= -8

b= 85

c= 100

d= -3

e= 110

f= 150

Si tratta di una semplice funzione composta da due parabole rovesciate e da un punto di discontinuità per X = 12. Con facili calcoli si trova che il massimo della funzione coincide con il vertice della seconda parabola (X = 18.333…, Y = 1158.336) ed il minimo della funzione (sempre per X compresa tra 1 e 25) coincide con il punto di discontinuità (X = 12, Y = -32) appartenente alla prima parabola. Vediamo ora come si comporta Excel, a seconda delle tre opzioni disponibili per il risolutore:

1. Modello lineare, metodo del simplesso. Excel ci avverte, correttamente, che il modello non è lineare e che pertanto non può essere risolto con questa opzione.


2. Modello non lineare, metodo GRG. Il metodo porta alla soluzione corretta solo se partiamo da un punto sufficientemente vicino al massimo assoluto o al minimo assoluto. In generale non è in grado di trovare ne il massimo ne il minimo della funzione.


3. Modello evolutivo. Il metodo porta sempre alla soluzione corretta.

Vediamo ora come si comporta il metodo Montecarlo che esplora a caso (punto lilla sul grafico) i punti delle due parabole per X compreso tra 1 e 25 e memorizza Xmin e Ymin (in F13 e G13, punto rosso sul grafico) e Xmax, Ymax (in F14 e G14, punto verde sul grafico). Montecarlo è un po' brutale, ma allo stesso tempo consente sia una ricerca di massimo che di minimo!

Ecco i risultati dopo solo 5,000 iterazioni:





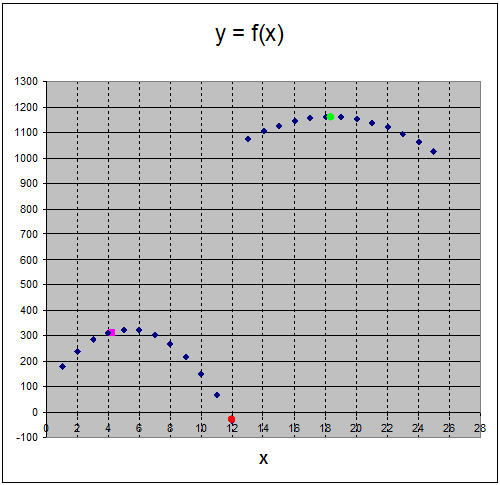
Con una approssimazione molto buona e in pochi secondi abbiamo calcolato sia il massimo che il minimo della funzione data. Naturalmente l'indubbio successo di Montecarlo, in questo caso, dipende dal fatto che la regione ammissibile, cioè quella in cui debbono essere cercate le soluzioni rispettando tutti i vincoli, è estremamente ristretta. In primo luogo perché si tratta di una regione monodimensionale (l'unica variabile indipendente è X); ed in secondo luogo perché la variabile X deve essere compresa tra limiti stretti: 1 e 25.

Il lettore interessato, scaricando il file Excel potrà effettuare nuove simulazioni, sia sulla funzione indicata sia su funzioni nuove monodimensionali di suo interesse. La nuova funzione dovrà essere digitata nella cella G15, mentre i limiti inferiori e superiori per la generazione dei numeri casuali nelle celle E15 e H15.



Nota Bene

Nel Menu Strumenti/Opzioni/Calcolo dovrà essere attivata la cella iterazioni, ponendo a 1 il numero massimo delle iterazioni.

Caso 1: Investimento in Titoli.

La dottoressa Pamela cessa la sua attività lavorativa dipendente, con una liquidazione di 100,000 Eur e si pone il problema di come investire al meglio i suoi risparmi per i prossimi 5 anni in attesa di future decisioni. Pamela ritiene di dover tenere almeno 20,000 Eur nel Conto corrente(CC), come tutela da eventuali imprevisti. Non amando molto i rischi, in azioni non intende investire più di 25,000 Eur.

Quindi i restanti 55,000 Eur sono da ripartire tra obbligazioni e titoli di stato (B1,B2)

Il suo consulente finanziario le consiglia di diversificare l'investimento azionario su due titoli: Il primo A1 che garantisce ottime cedole (8%), ma che essendo un po' meno sostenibile sul medio/lungo periodo consiglia di contenere entro i 10,000 Eur, il secondo (A2) un po' meno redditizio (cedola al 5%), ma più solido e sostenibile, per il rimanente della quota azionaria. Per quanto riguarda la quota obbligazionaria Il consulente caldeggia dei Bond (B1) a 5 anni di un campione energetico che offre rendimenti del 3%, ma la signora Pamela, che ha anche convinzioni patriottiche, decide di destinare almeno 15.000 Eur ai titoli di stato (B2) che rendono il 2%.

La Dottoressa Pamela, si rivolge al suo amico Igor, cultore di matematica applicata e di ricerca operativa, esponendogli i suoi obiettivi e pregandolo di darle un consiglio sul modo migliore per perseguirli. Igor prende carta e matita e rapidamente scrive:

A1 + A2 + B1 + B2 + CC = 100,000 Eur

0 <= A1 <= 10,000

0 <= A2 <= 15,000

0 <= B1 <= 30,000

15,000 <= B2 <= 25,000

20,000 <= CC

"Vedi - spiega Igor - questi sono i tuoi obiettivi primari (o i tuoi limiti/vincoli). Soddisfatti questi, suppongo tu voglia poi massimizzare le tue cedole annue. Dunque la tua funzione obiettivo Y è:

Y = 8%*A1+ 5%*A2 + 3%*B1+ 2%*B2 + 0%*CC

Questo è un semplice caso di programmazione lineare facilmente risolvibile con il metodo del Simplesso disponibile anche con il risolutore di Excel". Esaminando meglio il problema Igor aggiunge: "Guarda, Pamela, non serve neanche scomodare il simplesso. La soluzione al tuo problema è:

A1 = 10,000

A2 = 15,000

B1 = 30,000

B2 = 25,000

CC = 20,000

____________

Tot = 100,000 Eur Con rendita annua Y = 2,950 Eur

"Come hai fatto?" Esclama Pamela. "Guarda è semplice tu vuoi 20.000 Eur sul Conto Corrente che però non ti rende niente (0% nella funzione obiettivo) dunque altri soldi non conviene lasciarli li. Poiché i titoli danno comunque un rendimento (8%, 5%, 3%, 2%) annuo positivo, e poiché la somma dei limiti superiori è esattamente 80.000 Eur, quanto resta della tua liquidazione, dopo il deposito nel C.C., conviene investirlo nei titoli, al livello massimo consentito dai limiti prioritari che tu stessa hai posto.

Sai che ti dico, Pamela: poiché il tuo problema è risolto in modo ottimale, vorrei usare i dati numerici del tuo caso per illustrare cosa riesce a fare il metodo Montecarlo. Sto preparando un articolo per un sito di matematica e credo che il Caso sia interessante. Ho preparato un foglio Excel (Montecarlo e Ottimizzazione) e presto ti mostrerò i risultati".







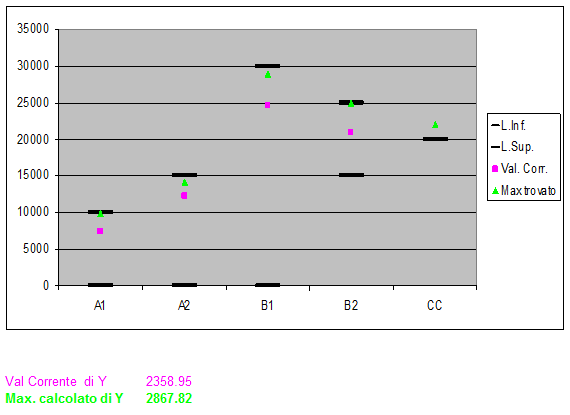
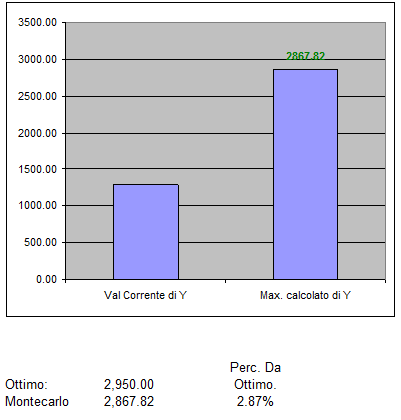
"Bene - commenta Igor - Montecarlo ha trovato una soluzione che dista solo del 2,87% dall'ottimo teorico. In pratica annualmente dovresti rinunciare a circa 82 Eur. Il metodo però ti permette, ovviamente il suggerimento è casuale e non intenzionale, di aumentare di circa 2,000 Eur la tua riserva sul Conto Corrente. Adesso sta a te scegliere, tra me e Montecarlo!".

Caso 2: Additivi ed edulcoranti di un farmaco.

Questo caso è stato ripreso e adattato dal testo di Conley pag. 112, citato in bibliografia.

Molti pazienti, a causa di loro malattie croniche, debbono prendere dei farmaci ogni giorno per il resto della loro vita. Per questo motivo si è deciso di cercare di migliorare (nel rispetto dei principi attivi necessari al farmaco e della non tossicità degli additivi) il gusto delle pillole da ingerire. Sono state proposte ai pazienti diverse dosi di due additivi (X1 e X2) e di un dolcificante (X3). I pareri dei pazienti sono stati poi raccolti e tradotti in termini quantitativi in modo da permettere successive analisi statistiche. Le analisi di regressione sulle preferenze (Y) dei pazienti hanno permesso di evincere la seguente funzione non lineare Y = Y (Xi):

Y(Xi) = 1000 - 0.009*x1*x3 + 40*x2 - 0.86*x3^2+ 90*x3 + 0.006*x1*x2 + 0.01*x2*x3 - x1^2 + 60*x1 - 1.1*x2^2

Che deve essere massimizzata all'interno dei vincoli:

0 <= Xi <= 95 con Xi intero (i = 1,2,3) che rappresenta le dosi degli additivi e dell'edulcorante.





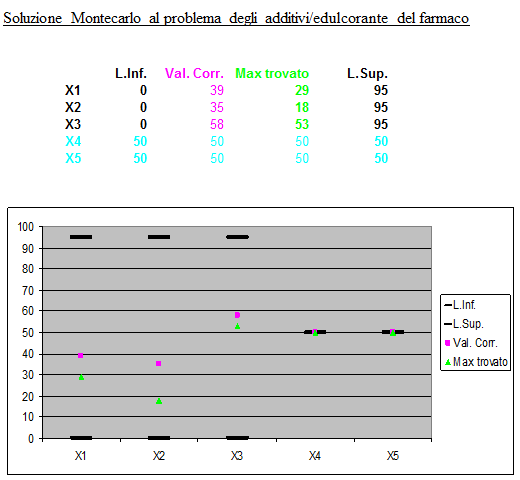
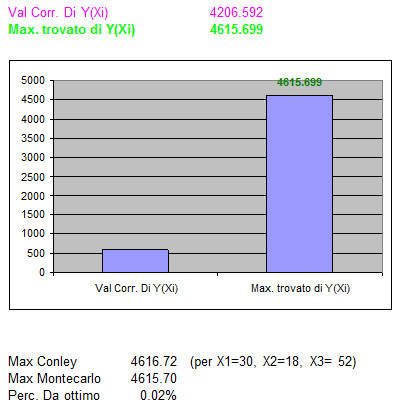
Si noti che in questo Caso, essendo il problema a numeri interi, invece della funzione CASUALE() è stata utilizzata la funzione CASUALE.TRA(0;95).

Montecarlo ha consentito di trovare una soluzione molto prossima all'ottimo assoluto (differenza percentuale dello 0.02%). La soluzione Montecarlo espressa in numero di unità degli additivi e dell'edulcorante (X1 = 29, X2 = 18, X3 =53) ha permesso di migliorare il gusto del farmaco di circa il 46%.

Caso 3: Migliorare la qualità della vita.

Questo Caso è stato ripreso e adattato dal testo di Conley pag. 121, citato in bibliografia.

Un gruppo di ricercatori di una estesa regione ha studiato per anni la salute della popolazione. L'obiettivo era quello di individuare le circostanze ambientali e i comportamenti individuali che potevano ridurre l'insorgere di una specifica malattia. Una analisi statistica preliminare ha consentito di individuare quattro variabili, indipendenti e fondamentali, per comprendere l'insorgere della malattia:

X1: dimensione delle città in cui si vive. Con X1 = 0 rappresentante una città con meno di 10,000 abitanti ed X1 = 100 rappresentante qualunque città con più di un milione di abitanti.

X2: livello della attività sportiva della popolazione in una scala compresa tra 0 è 100

X3: tipo di dieta, che può contenere da 10 a 40 unità giornaliere di un particolare tipo di vitamina.

X4: consumo di alcolici misurato tra: 0 (nessun consumo) e 100 (consumo moderato).

Dunque i vincoli sono:

0 <= X1, X2, X4 <= 100 e 10 <= X3 <= 40 Xi = intero per (i = 1,2,3,4)

L'analisi di regressione sui dati rilevati ha portato a definire una curva di risposta che rappresenta, rispetto a una media del 100% di prendere la malattia, la capacità di ridurre il rischio operando sulle quattro variabili elencate. Nella funzione obiettivo da massimizzare riportata sotto ogni punto percentuale è posto uguale a 1000.

Obj. Func: Max! Y(Xi) = 925 - 0.5*x1*x4 + x2^2 -10*x2 + x3^2 - 56*x3 + x4^2 - 20*x4



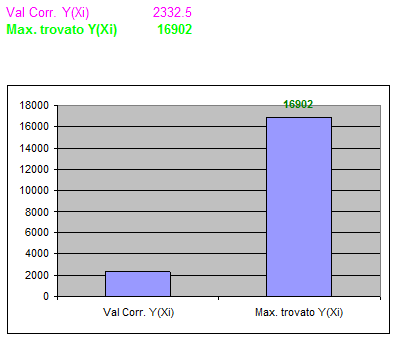
Dunque secondo Montecarlo ognuno può ridurre del 16.902% l'eventualità di contrarre la specifica malattia con le seguenti strategie:

X1 = 1 (vivere in una piccola città).

X2 = 100 (fare molto esercizio fisico).

X3 = 28 (unità giornaliere di vitamina da assumere).

X4 = 100 (consumare alcol, ma in modo moderato).



Conclusioni:

Il metodo Montecarlo, utilizzato nella ottimizzazione può portare a soluzioni sub-ottimali molto buone con semplicità ed efficienza. Ci si può però chiedere quali possono essere le strade, migliorando l'algoritmo, per una ricerca più precisa ricerca dell'ottimo assoluto. A parere di chi scrive le vie possibili sono tre:

1. Effettuare diverse simulazioni restringendo man mano i vincoli delle variabili attorno alla miglior soluzione trovata.


2. Ricorrere ad un algoritmo che provvede automaticamente a restringere la regione ammissibile dopo aver trovato una soluzione soddisfacente (Montecarlo multistage programs).


3. Abbinare Montecarlo con altri sistemi che prevedono una miglior convergenza alla soluzione ottima assoluta (ad esempio gli algoritmi evolutivi).

Infine si vuole far cenno a un aspetto importante del metodo: il numero delle replicazioni da effettuare. La precisione di Montecarlo cresce con la radice quadrata delle "n" replicazioni, dunque meno che linearmente. Per intenderci per raddoppiare la precisione (cioè la riduzione dell'errore) bisogna quadruplicare il numero delle replicazioni. D'altro canto per decidere quando fermare le iterazioni basta calcolare l'andamento delle medie delle variabili al crescere di n. Quando gli andamenti tendono a stabilizzarsi (diventano quasi asintotici) non c'è motivo di continuare con le replicazioni. (Vedi in proposito, su Matematicamente.it, l'articolo "Executive Jet" di Hume, citato in bibliografia).

Bibliografia

• W. Conley, "Optimization: A Simplified Approach", Petrocelli, New York 1981.


• J.P. Ignizio, "Goal Programming and Extensions" Lexin\gton Books, Toronto 1979.


• A.G.B. Tettamanzi "Algoritmi Evolutivi: concetti ed applicazioni", 2005.


• http://www.dmi.unict.it/mpavone/nc-cs/materiale/tettamanzi-2005.pdf


• V. Ozzola, "Divertimento su temi di Ricerca Operativa", Alinea Editrice, Firenze, 2007.


• M. Chiodi, "Tecniche di Simulazione in Statistica", Univ. Palermo.


• E. Degiuli, "I metodi Montecarlo I° e II° parte", 2015.


• http://www.mathisintheair.org/wp/2015/10/i-metodi-monte-carlo-prima-parte/


• http://www.mathisintheair.org/wp/2015/12/i-metodi-monte-carlo-seconda- parte/


• R.Chiappi, "Introduzione al metodo Montecarlo", 2015. www.matematicamente.it


• R.Chiappi, " Montecarlo nel Project Management", 2015. www.matematicamente.it


• Hume, " Motoscafo", 2015. www.matematicamente.it


• Hume, " Executive Jet", 2015. www.matematicamente.it