Teoremi delle corde, secanti e tangenti

I seguenti teoremi delle corde, secanti e tangenti di una circonferenza, sono conseguenze del primo criterio di similitudine dei triangoli.

Teorema delle corde

Due corde di una circonferenza che si intersecano vengono divise dal punto di intersezione in modo che i segmenti di una sono gli estremi e i segmenti dell'altra sono i medi di una stessa proporzione.

Ad esempio, consideriamo la circonferenza in figura, possiamo stabilire una proporzione di questo tipo fra i segmenti creati dall'intersezione delle corde:

AE : DE = CE : BE

Ciò è possibile perché i triangoli AEC e DEB sono triangoli simili.

Mentre il teorema delle corde si applica nel caso di corde incidenti, il teorema delle secanti è utile nel caso in cui le corde della circonferenza non si intersecano; si considerano, quindi, i loro prolungamenti, che si intersecano al di fuori dalla circonferenza.

Teorema delle secanti

Se da un punto esterno a una circonferenza si conducono due rette ad essa secanti, i segmenti di una secante compresi tra tale punto e i punti di intersezione con la circonferenza e gli analoghi segmenti dell'altra secante sono rispettivamente gli estremi i medi di una stessa proporzione.

Ad esempio, considerando la circonferenza in figura, possiamo stabilire questa proporzione:

AC : AE = AD : AB

Possiamo mettere in proporzione questi segmenti perché i triangoli ACD e AEB, che li hanno per lati, sono triangoli simili.

Possiamo estendere il teorema delle secanti al caso in cui una di esse sia tangente alla circonferenza:

Teorema della tangente e della secante

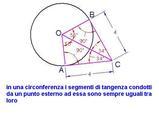
Se da un punto esterno ad una circonferenza si conducono una retta tangente ed una secante, il segmento di tangente è medio proporzionale tra i segmenti della secante compresi tra il punto considerato e i punti in cui la secante interseca la circonferenza.

Considerando la circonferenza in figura, abbiamo la seguente proporzione:

AC : AT = AT : AB

La proporzione è valida poiché i triangoli ACT e ATB sono simili.