Indice
Angoli al centro e alla circonferenza - Teoria
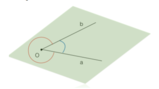
Angolo al centro - definizione
Consideriamo una circonferenza di centro
[math]O[/math]
.Su di essa prendiamo inoltre due punti:
[math]A, B[/math]
.Allora diremo che
[math]\widehat{AOB}[/math]
è un angolo al centro in quanto ha il vertice nel centro della circonferenza.
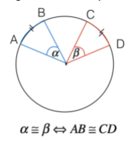
Angolo alla circonferenza - Definizione
Prendiamo adesso, sempre sulla circonferenza, un punto C.
L'angolo[math]\widehat{ACB}[/math]
è detto angolo alla circonferenza corrispondente all'angolo al centro se i punti sulla circonferenza compresi tra i due angoli sono gli stessi.Viceversa, l'angolo
[math]\widehat{AOB}[/math]
è detto angolo al centro corrispondente all'angolo alla circonferenza[math]\widehat{ACB}[/math]
.
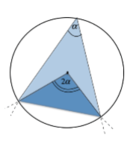
Teorema dell'angolo al centro e dell'angolo alla circonferenza
L'ampiezza di un angolo al centro è equivalente al doppio dell'ampiezza dell'angolo alla circonferenza ad esso corrispondente.
Dimostriamo adesso il teorema.
Dimostrazione Teorema
Il triangolo
[math]OAB[/math]
è isoscele in quanto OA=OB (sono entrambi raggi!), poniamo quindi [math]\widehat{OAB}=\widehat{OBA}=\alpha[/math]
.Anche i triangoli
[math]OBC[/math]
e [math]OCA[/math]
sono isosceli perché [math]OB=OC=OA[/math]
, pertanto possiamo porre [math]\widehat{OCA}=\widehat{OAC}=\gamma[/math]
e [math]\widehat{OBC}=\widehat{OCB}=\beta[/math]
.Notiamo che
[math]\widehat{ACB}=\gamma+\beta[/math]
.Sfruttando il fatto che in un triangolo la somma degli angoli interni vale un angolo piatto si ha
[math]2\alpha+2\beta+2\gamma=180°[/math]
pertanto [math]\alpha+\beta+\gamma=90°[/math]
e quindi [math]\widehat{ACB}=90-\alpha[/math]
.Ma allora per differenza di angoli,
[math]\widehat{AOB}=180°-\alpha-\alpha=180°-2\alpha[/math]
ed effettivamente [math]2(90-\alpha)=180-2\alpha[/math]
, come volevamo dimostrare.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
