Sui lati
[math]\bar(AB),\bar(BC),\bar(CA)[/math]
di un triangolo equilatero si prendono i punti rispettivamente
[math]E,F,G[/math]
in modo
che
[math]\bar(AE)~=\bar(BF)~=\bar(CG)[/math]
.Dimostrare che
[math]hat{EFG}[/math]
è un triangolo equilatero.
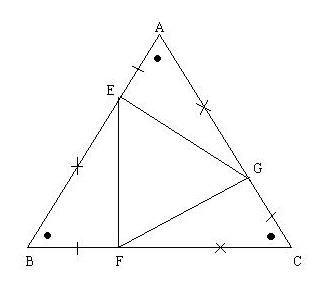Ipotesi[math]\bar(AB)~=\bar(BC)~=\bar(CA)[/math]
[math]\bar(AE)~=\bar(BF)~=\bar(CG)[/math]
Dimostrazione
Dobbiamo dimostare che
[math]\bar(EF)~=\bar(FG)~=\bar(EG)[/math]
I triangoli
[math]hat{AEG},hat{BEF},hat{FCG}[/math]
sono congruenti, infatti
[math]\bar(AE)~=\bar(BF)~=\bar(CG)[/math]
per costruzione
[math]hatA~=hatB~=hatC[/math]
perchè
[math]hat{ABC}[/math]
è un triangolo equilatero
[math]\bar(AG)~=\bar(BE)~=\bar(FC)[/math]
perchè differenza di segmenti congruenti, infatti
[math]\bar(AG)=\bar(AC)-\bar(CG)[/math]
[math]\bar(BE)=\bar(BA)-\bar(AE)[/math]
[math]\bar(FC)=\bar(BC)-\bar(BF)[/math]
Sono quindi congruenti per il primo criterio; di conseguenza hanno tutti gli elementi congruenti,
in particolare
[math]\bar(EF)~=\bar(FG)~=\bar(EG)[/math]
.
Pertanto il triangolo
[math]hat{EFG}[/math]
è equilatero.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
