Stabilisci mediante confronto grafico il numero delle soluzioni della seguente equazione, se esistono, e per ciascuna di esse individua un intervallo che le contiene.
Svolgimento
Scomponiamo la scrittura in due equazioni di funzioni note e mettiamole a sistema:
left{ \begin{array}{rl}
y = 2^x &\
y = 1 - x^2 &
end{array}\right.
[math][/math]
Abbiamo quindi la prima che è la funzione esponenziale, per la quale, essendo la base maggiore di
,
è asintoto orizzontale sinistro; l'altra, invece, è l'equazione di una parabola, di cui possiamo trovare subito il vertice:
Sostituendo questo valore di x all'equazione della parabola ricaviamo l'ordinata del vertice:
Quindi:
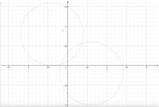
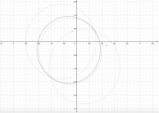
Rappresentiamo le curve sul piano cartesiano:
Ingrandendo l'immagine, possiamo notare i punti di intersezione fra le due curve.
Possiamo dire con certezza che l'equazione avrà due soluzioni, delle quali sappiamo che la prima è
, poiché uno dei punti di intersezione fra le due curve è proprio nel punto
.
Dell'altra soluzione non conosciamo con esattezza il valore, ma possiamo stabilire un intervallo in cui siamo certi che si troverà la seconda soluzione:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
