Secondo teorema sulle corde
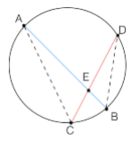
Teorema: "Se in una circonferenza un diametro è perpendicolare ad una corda, allora la corda, l'angolo al centro e l'arco corrispondenti risultano divisi a metà da tale diametro."
Dimostrazione:
Ip:
[math]AB⊥CD[/math]
.[math]AB[/math]
è diametro.[math]CD[/math]
è corda.Th:
[math]CM=MD[/math]
.[math]COB=BOD[/math]
.[math]CB=BD[/math]
.Consideriamo due funzioni:
[math]f(AB):OC=r[/math]
e [math]f'(AB):OD=r[/math]
.La funzione rispetto all'asse passante per
[math]AB[/math]
che risulta essere diametro, sarà l'uguaglianza tra le due funzioni:
[math]f(AB)=f'(AB):OC=OD=r[/math]
.Da qui otteniamo che il punto
[math]O[/math]
è equidistante sia dall'estremo [math]C[/math]
che dall'estremo [math]D[/math]
, ma esso è anche centro della circonferenza, pertanto [math]OC[/math]
ha la stessa distanza di [math]OD[/math]
e quindi sono congruenti e sono appunto raggi, poiché congiungono il centro con un punto appartenente alla circonferenza stessa. Il triangolo [math]COD[/math]
è isoscele sulla base [math]CD[/math]
la quale sottende l'arco [math]CD[/math]
.In un triangolo isoscele l'asse coincide con l'altezza, quindi
[math]OM[/math]
è altezza, ma allo stesso modo coincide con la mediana, e dunque:
[math]CM=MD[/math]
, e coincide con la bisettrice, quindi: [math]COB=BOD[/math]
. a angoli al centro congruenti, in una circonferenza, corrispondono archi congruenti, quindi [math]CB=BD[/math]
. Come volevasi dimostrare.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
