Scrivere l'equazione della retta
[math]r[/math]
passante per l'origine [math]O(0;0)[/math]
e per il punto [math]A(4;6)[/math]
Verificare che
[math]B(-2;-3) \in r[/math]
e che [math]C(2;7) \notin r[/math]
Svolgimento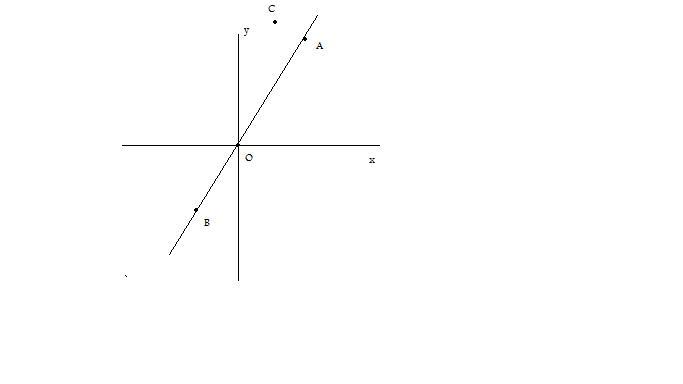
La retta
[math]r[/math]
, passando per l'origine, sarà rappresentata da un'equazione del tipo [math]y=mx[/math]
.Poichè la retta deve passare per
[math]A(4;6)[/math]
, le coordinate di questo punto devono verificare l'equazione:[math]6=m*(4) => m=6/4=3/2[/math]
.L'equazione di
[math]r[/math]
sarà quindi: [math]y=3/2x[/math]
che possiamo riscrivere come [math]2y-3x=0[/math]
.
Sostituendo nella disequazione al posto di
[math]x[/math]
e [math]y[/math]
le coordinate di [math]B[/math]
verifichiamo se tale punto appartiene a [math]r[/math]
.
[math]2y-3x=0[/math]
diviene [math]2(-3)-3(-2)=0 => -6+6=0 => 0=0[/math]
.L'equazione è verificata, pertanto
[math]B \in r[/math]
Con lo stesso procedimento verifichiamo l'appartenenza di [math]C[/math]
ad [math]r[/math]
[math]2y-3x=0[/math]
diviene [math]2*7-3*2=0 => 14-6=0 => 8=0[/math]
L'equazione non è verificata, pertanto [math]C \notin r[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
