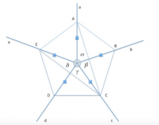
Quattro semirette di origine
[math]O[/math]
si susseguono nell'ordine [math]a[/math]
, [math]b[/math]
, [math]c[/math]
, [math]d[/math]
, e gli angoli [math]ad[/math]
e [math]bc[/math]
hanno la stessa bisettrice [math]s[/math]
. Prendi su [math]a[/math]
e [math]d[/math]
rispettivamente i segmenti [math]OA = OD[/math]
e su [math]b[/math]
e [math]c[/math]
rispettivamente i segmenti [math]OB = OC[/math]
.Dimostra che
[math]ac = bd[/math]
, [math]AB = CD[/math]
e [math]AC = BD[/math]
.
Svolgimento
Consideriamo gli angoli[math]hat{AOB}[/math]
e [math]hat{COD}[/math]
. Essi sono congruenti perché opposti al vertice.Ora consideriamo i triangoli
[math]COD[/math]
e [math]BOA[/math]
. Essi hanno:-
[math]DO = AO[/math]per ipotesi;
-
[math]OC = BO[/math]per ipotesi;
-
[math] hat{AOB} = hat{COD}[/math]perché angoli opposti al vertice;
[math]COD[/math]
e [math]BOA[/math]
sono congruenti.In particolare risulta che
[math]AB = CD [/math]
.Di conseguenza
[math]AC = BD[/math]
perché somme di lati congruenti.Gli angoli formati dalle rette
[math]ac[/math]
e [math]bd[/math]
sono congruenti perché somme di angoli congruenti; si ha infatti che:-
[math] hat{AOB} = hat{COD}[/math]perché angoli opposti al vertice;
- l'angolo [math]bc[/math]è congruente all'angolo[math]ad[/math], anch'essi opposti al vertice.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
