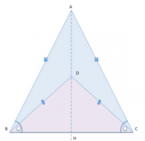
Dato un segmento
[math]BC[/math]
prendi, in uno stesso semipiano di origine [math]BC[/math]
, due punti [math]A[/math]
e [math]A'[/math]
, in modo che sia [math] AB = A'C [/math]
, [math]AC = A'B[/math]
e [math]AB > AC[/math]
. Sia [math]Q[/math]
il punto d'intersezione dei segmenti [math]AB[/math]
e [math]A'C[/math]
. Dimostra che il triangolo [math]BCQ[/math]
è isoscele e che i due triangoli [math]A'BQ[/math]
e [math]ACQ[/math]
sono congruenti.
Svolgimento
Consideriamo i triangoli[math]ACB[/math]
e [math]A'BC[/math]
. Essi hanno:-
[math] A'B = AC [/math]per ipotesi;
-
[math]BC[/math]in comune;
-
[math] AB = A'C [/math], per ipotesi.
[math]ACB[/math]
e [math]A'BC[/math]
sono congruenti.Si avrà quindi che
[math]hat{QBC} = hat{QCB}[/math]
, [math]hat{ACB} = hat{A'BC}[/math]
, [math]hat{BA'C} = hat{CAB}[/math]
.Il triangolo
[math]BCQ[/math]
è quindi isoscele, perché avente gli angoli alla base congruenti [math]( hat{QBC} = hat{QCB}) [/math]
. Di conseguenza, esso avrà anche due lati congruenti: [math]QB = QC [/math]
.Ora consideriamo i triangoli
[math]A'BQ[/math]
e [math]ACQ[/math]
. Essi hanno:-
[math]hat{BA'C} = hat{CAB}[/math]per la precedente dimostrazione;
-
[math]hat{A'BQ} = hat{ACQ}[/math]perché differenze di angoli congruenti;
-
[math]A'B = AC [/math]per ipotesi.
[math]A'BQ[/math]
e [math]ACQ[/math]
sono congruenti.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
