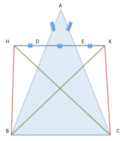
Due triangoli isosceli
[math]ABC [/math]
e
[math]BCD[/math]
hanno in comune la base
[math]BC[/math]
e i vertici
[math]A[/math]
e
[math]D[/math]
sono situati nello stesso semipiano di origine
[math]BC[/math]
, in modo che il triangolo
[math]BCD[/math]
sia contenuto in
[math]ABC[/math]
. Dimostra che la semiretta di origine
[math]A[/math]
e passante per
[math]D[/math]
è la bisettrice degli angoli al vertice dei due triangoli.

Svolgimento
Consideriamo i triangoli
[math]ADB[/math]
e
[math]ADC[/math]
; essi hanno:
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l'angolo fra essi compreso congruente, i triangoli
[math]ADB[/math]
e
[math]ADC[/math]
sono congruenti.
Essendo i due triangoli congruenti, si ha che
[math]\hat{BAH} = \hat{CAH}[/math]
e
[math]\hat{ADB} = \hat{ADC}[/math]
.
Ora consideriamo i triangoli
[math]DBH[/math]
e
[math]DCH[/math]
; possiamo affermare che
[math]\hat{BHD} = \hat{CDH}[/math]
perché angoli supplementari di angoli congruenti;
Abbiamo quindi dimostrato che la semiretta di origine
[math]A[/math]
e passante per
[math]D[/math]
è la bisettrice degli angoli al vertice dei due triangoli.








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo