[math]D \subset \mathbb{R}^2[/math]
il dominio di definizione della funzione
[math]f(x,y) = \sqrt{x^2 - 4} \cdot \log{(36 - 4x^2 - 9y^2)}[/math]
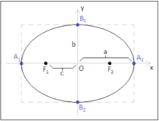
Disegnarlo, determinare la frontiera e stabilire se
[math]D[/math]
è aperto, chiuso, limitato, compatto, e da quante componenti connesse è composto.
Una radice quadrata è definita quando il radicando è non negativo, un logaritmo invece ha senso se l'argomento è positivo, pertanto il dominio della funzione si può trovare risolvendo il seguente sistema
[math]\begin{cases} x^2 - 4 \ge 0 \\ 36 - 4x^2 - 9y^2 & \gt; 0 \end{cases} = \begin{cases} x \le -2 \quad \vee \quad x \ge 2 \\\frac{x^2}{9} + \frac{y^2}{4}
Quindi
[math]D = \{ (x,y) \in \mathbb{R}^2: x^2 - 4 \ge 0, \frac{x^2}{9} + \frac{y^2}{4}
Il dominio
Infine
La frontiera dell'insieme è
[math]\partial D = \{(-2,y) \in \mathbb{R}^2: - \sqrt{\frac{28}{9}} \le y \le \sqrt{\frac{28}{9}} \} \cup \{ {2,y} \in \mathbb{R}^2: - \sqrt{\frac{28}{9}} \le y \le \sqrt{\frac{28}{9}} \} \cup \{ (x,y) \in \mathbb{R}^2: \frac{x^2}{9} + \frac{y^2}{4} = 1, x \le -2 \} \cup \{ (x,y) \in \mathbb{R}^2: \frac{x^2}{9} + \frac{y^2}{4} = 1, x \ge 2 \}[/math]
Dato che
[math]\partial D \cap D \ne \emptyset[/math]
, e che la frontiera di [math]D[/math]
non è interamente contenuta in [math]D[/math]
, l'insieme non è aperto né chiuso.Il dominio
[math]D[/math]
è un insieme limitato, esiste infatti un intorno sferico aperto dell'origine (ad esempio di raggio [math]10[/math]
) che lo contenga propriamente.Infine
[math]D[/math]
non è connesso per archi, ma possiede due componenti connesse.FINE
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
