vuoi
o PayPal
tutte le volte che vuoi
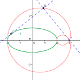 Si dice podaria di una curva C rispetto a un punto A (detto polo) il luogo dei piedi delle perpendicolari condotte da A alle tangenti alla curva stessa; la curva C è detta antipodaria della podaria ottenuta. In questo breve articolo si determina l'equazione della podaria a un'ellisse.
Si dice podaria di una curva C rispetto a un punto A (detto polo) il luogo dei piedi delle perpendicolari condotte da A alle tangenti alla curva stessa; la curva C è detta antipodaria della podaria ottenuta. In questo breve articolo si determina l'equazione della podaria a un'ellisse. Francesco Camia, Podaria di una curva rispetto a un punto, agosto 2012
SULLA PODARIA DI UNA CURVA RISPETTO A UN PUNTO
di Francesco Camia
Si dice podaria di una curva C rispetto a un punto A (detto polo) il luogo dei piedi delle per-
pendicolari condotte da A alle tangenti alla curva stessa; la curva C è detta antipodaria della
podaria ottenuta.
Supponiamo che la curva C sia piana e sufficientemente regolare, in particolare che in ogni suo
punto essa possieda una sola retta tangente.
In un piano, riferito ad un sistema d’assi cartesiani ortogonali, consideriamo la curva (conica) C di
2 2 l’equazione della sua podaria rispetto al punto
equazione x + 4 y = 4 e ci proponiamo di trovare
A=(3; 0) . L’equazione di C può essere scritta, dividendone i due membri per 4, nella forma
, da cui si nota che C è un’ellisse riferita a centro e assi, con i fuochi sull’asse x
(reale),
di misura 2 sull’asse x); C è pertanto una curva algebrica del se-
e semiassi di misura 2 e 1 (quelli
condo ordine priva di punti multipli che quindi possiede un’unica tangente in ogni suo punto.
Indicando con P un generico punto dell’ellisse C, siano la tangente in P all’ellisse,
a b la perpen-
il punto d’intersezione delle rette
dicolare ad a condotta per A, B a e b. La podaria in questione è il
P sull’ellisse
luogo descritto dal punto B al variare del punto C.
Per determinare l’equazione di questo luogo, procederemo con il metodo di eliminazione dei
parametri.








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









