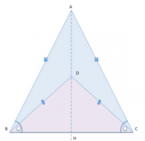
La figura a fianco rappresenta il tragitto fatto da Pluto per andare dalla sua cuccia, posta in
, al bar, posto in
. I tre segmenti
,
e
sono lunghi
metri ciascuno. Se l'angolo
(interno al triangolo
) è di
e l'angolo
(interno al triangolo
) è di
, quanto dista in linea retta il bar dalla cuccia?
Svolgimento
Sappiamo per ipotesi che:
Il problema chiede di determinare la distanza fra la cuccia posta nel punto
e il bar posto nel punto
, cioè la lunghezza del segmento
.
Poiché sappiamo già che
misura
, dobbiamo solo trovare la lunghezza di
.
Consideriamo il triangolo
: possiamo calcolare l'ampiezza dell'angolo
sottraendo all'angolo piatto l'ampiezza di
.
Quindi:
Il triangolo
ha quindi due angoli di
, e avrà di questa ampiezza anche il terzo.
Di conseguenza, il triangolo in questione è equilatero.
Essendo i suoi lati tutti uguali, possiamo affermare che
.
Di conseguenza la distanza che separa il punto
dal punto
è
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
