Le geometrie non euclidee
Le geometrie non euclidee partono da postulati opposti a quello di Euclide sulla rette parallele, in particolare dalle due negazioni possibili del V postulato .
Un modo equivalente per esprimere questo postulato di Euclide è il seguente:
P1) In un piano, per un punto esterno a una retta data esiste un'unica retta passante per il punto dato e parallela alla retta data.
Un teorema che consegue da questo postulato è il seguente:
T1) In un triangolo, la somma degli angoli interni è 180°.
Nel 1829, N. Lobacevskij , e più o meno contemporaneamente l'ungherese J. Bolyai , costruirono una geometria, risultata poi altrettanto coerente matematicamente di quella di Euclide, secondo la quale
P2) per un punto esterno a una retta data passa più di una retta parallela (se ne esiste più di una ne esistono infinite).
Come conseguenza,
T2) in un triangolo, la somma degli angoli interni è minore di 180°
Nel 1854, B. Riemann , in uno studio globale sulla geometria, ipotizzo la possibilità di una terza geometria, nella quale
P3) per un punto esterno a una retta data non passa alcuna parallela.
Come conseguenza,
T3) in un triangolo, la somma degli angoli interni è maggiore di 180°.
Le tre geometrie sono state più correttamente definite da F. Klein , rispettivamente, geometria parabolica, iperbolica ed ellittica.
Per immaginare le due geometrie distinte da quella euclidea si può fare ricorso a dei 'modelli'.
Per la geometria ellittica o riemanniana, Invece del piano consideriamo la superficie di una sfera e traduciamo gli elementi geometrici del piano in corrispondenti elementi geometrici sulla superficie della sfera.
I punti del piano corrispondono a punti della superficie della sfera. Le rette del piano corrispondono alle circonferenze massime della superficie sferica. In generale, si fanno corrispondere alle rette del piano le linee geodetiche di una superficie curva. Queste ultime infatti conservano la principale caratteristica delle rette e precisamente sono le linee più brevi che sulla superficie congiungono due punti dati. Sulla superficie della sfera le geodetiche sono proprio le circonferenze massime, cioè quelle circonferenze che si ottengono intersecando la superficie della sfera con piani passanti per il centro della sfera. Esempi familiari sono i meridiani e l'equatore, non lo sono i paralleli.
Sulla superficie della sfera non esistono 'rette' o meglio geodetiche che non si incontrano, quindi non esistono parallele.
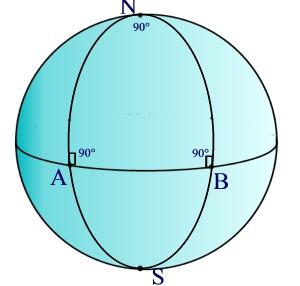 Nella figura sono rappresentati due meridiani perpendicolari all'equatore e che si incontrano perpendicolarmente al polo Nord. Si vede che la somma degli angoli interni del triangolo curvilineo ABN è 270°. In generale la somma degli angoli interni di un triangolo di questo tipo è sempre maggiore di 180° e non è costante per tutti i triangoli. Mentre nella geometria euclidea la somma degli angoli interni di un triangolo è sempre 180°, nella geometria ellittica la somma degli angoli interni del triangolo è variabile e dipende dalla grandezza del triangolo.
Nella figura sono rappresentati due meridiani perpendicolari all'equatore e che si incontrano perpendicolarmente al polo Nord. Si vede che la somma degli angoli interni del triangolo curvilineo ABN è 270°. In generale la somma degli angoli interni di un triangolo di questo tipo è sempre maggiore di 180° e non è costante per tutti i triangoli. Mentre nella geometria euclidea la somma degli angoli interni di un triangolo è sempre 180°, nella geometria ellittica la somma degli angoli interni del triangolo è variabile e dipende dalla grandezza del triangolo. 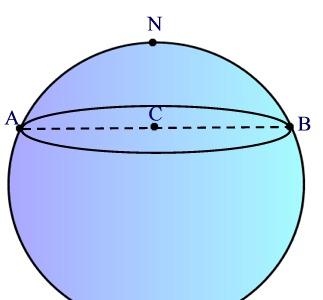
Un'altra caratteristica di questo tipo di geometria è che il rapporto tra circonferenza e raggio è minore di PIGRECO.
Infatti, la circonferenza di diametro AB non ha centro in C ma in N, ricorda che siamo sulla superficie della sfera, mentre C è posto dentro la sfera. Poiché evidentemente l'arco AN è maggiore del segmento AC, il rapporto tra la circoferenza AB e il suo raggio AN è minore di PIGRECO.
Un modello intuitivo, dadatticamente utile per la geometria iperbolica o di Lobacevskj è un po' più complesso. In particolare, non esiste un modello che rappresenti globalmente una geometria di questo tipo. Si può prendere una superficie a forma di sella, o meglio la pseudosfera (vedi scheda sulla pseudosfera di Beltrami ).
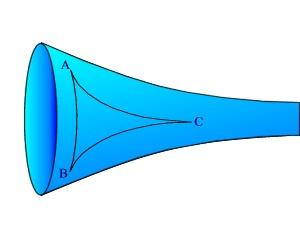
Il triangolo curvilineo ABC su un pezzo di pseudosfera è il corrispondente di un triangolo rettilineo del piano euclideo, perché è composto da linee geodetiche. La somma degli angoli interni di questo triangolo è minore di 180° e dipende dalla grandezza del triangolo.
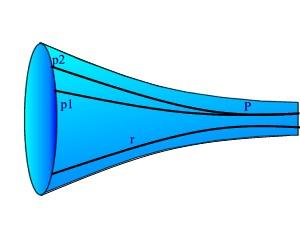
Per il punto P, esterno alla geodetica r, passano più geodetiche (p1 e p2) che non incontrano la geodetica r e che quindi sono parallele a r.
Antonio Bernardo
P. Parrini, Fisica e geometria dall'Ottocento a oggi , Loescher, Torino, 1979
P. Freguglia, Fondamenti storici della geometria, Feltrinelli, Milano,1982
R. Bonola, La geometria non euclidea, esposizione storico critica del suo sviluppo, Zanichelli, Bologna, 1906
R Trudeau, La geometria non euclidea, Bollati Boringheri, Torino, 1991







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo