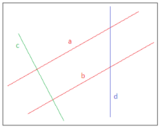
Il 5° postulato di Euclide, rappresentato in figura, recita: "Quando una retta incontra altre due rette e forma con esse dalla stessa parte angoli interni la cui somma è inferiore a due angoli retti, quelle due rette, prolungate all'infinito, devono incontrarsi dal lato dove si trovano gli angoli la cui somma è inferiore a due retti".
Quindi le due rette si incontrano sempre, da una parte o dall'altra, a meno che la somma degli angoli non sia esattamente uguale a 180°, in questo caso le due rette non si incontrano nè da una parte nè dall'altra: esse sono parallele.
Molti matematici, tra cui lo stesso Euclide, tentarono senza successo di ridurre questo postulato ad altri più evidenti, ma esso assieme a tutta la geometria greca fu considerato valido per circa 2100 anni fino a quando, Gauss ed altri, svilupparono geometrie che, pur totalmente coerenti, contraddicevano il 5° postulato.
Le geometrie non euclidee trovarono poi applicazione per risolvere alcuni problemi dello spazio-tempo posti dalla relatività generale di A.Einstein.
La geometria di Euclide è sempre viva e molte sono le applicazioni nell'ingegneria e nelle costruzioni. Nella logistica ricordo un programma che sviluppammo per dimensionare il numero di bettoline che dovevano trasportare i tubi necessari alla costruzione di una condotta sottomarina: usammo iterativamente il teorema di Pitagora generalizzato (Carnot). Nella gestione dei progetti dovevamo giustificare formule empiriche usate per le proiezioni a finire di tempi e costi: usammo con semplicità ed efficacia le proprietà dei triangoli simili.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
