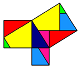Alcune dimostrazioni grafiche del teorema di Pitagora

DIMOSTRAZIONI GRAFICHE DEL TEOREMA DI PITAGORA

di Luciano Porta

“La geometria possiede due grandi tesori: uno è il teorema di

Pitagora; l’altro la divisione di una linea secondo il rapporto estremo

e medio. Possiamo paragonare il primo a una certa quantità d’oro, e

definire il secondo una pietra preziosa” Johannes Kepler

Molte sono le “dimostrazioni grafiche” del teorema di Pitagora. Spesso sono un felice connubio tra

geometria e arte. Alcune sono molto efficaci per “vedere” intuitivamente il teorema.

1. Dimostrazione antica

E’ forse la dimostrazione più conosciuta. Il quadrato grande può essere formato o dal quadrato costruito

sull’ipotenusa e da quattro triangoli rettangoli uguali o dai due quadrati costruiti sui cateti e da quattro

triangoli rettangoli uguali. 2. Dimostrazione di Bhaskara

Questa bellissima dimostrazione è di Bhaskara (1114 - 1185), grande matematico e astronomo indiano.

1

3. Dimostrazione di Leonardo da Vinci

La dimostrazione di Leonardo è geniale. Le due figure sono divise dalle diagonali verticali in parti uguali.

4. Dimostrazione di Airy

E’ probabilmente la più elegante dimostrazione. Traslando i triangoli rettangoli superiori, come indicato

dalle frecce, dal quadrato costruito sull’ipotenusa si ottengono i quadrati costruiti sui cateti. Sembra (da

“Il giardino di Archimede”) che questa dimostrazione sia stata ideata da G. B. Airy, astronomo

dell’osservatorio di Greenwich dal 1836 al 1881, intorno al 1855. Nella parte centrale della figura Airy

scrisse la poesia: I am, as you may see,

2 2

a + b – ab.

When two triangles on me stand,

Square of hypothenuse is plann’d;

But if I stand on them instead,

The squares of both sides are read.

2

5. Dimostrazione di Perigal

Fu proposta nel 1873 da Henry Perigal, agente di cambio inglese. Il punto A è il centro del quadrato.

6. Dimostrazione di Dekker

Fu pubblicata nel 1888 dallo scrittore olandese Edward Douwes Dekker con lo pseudonimo di Multatuli.

3