Classificare i fenomeni e scegliere le strategie migliori [Pareto]

Per Pareto le scienze economiche e sociali sono caratterizzate dalla forte interdipendenze di tutte le variabili, cosa che rende difficile le attività di previsione e di controllo. Questa situazione obbliga a ricorrere alla "logica matematica che sola può tener conto con ogni ampiezza della interdipendenza". Pareto si è effettivamente servito della matematica in economia e ne ha consigliato l'uso in sociologia, pur senza nutrire eccessive illusioni sulla portata pratica di tale consiglio. Per seguirlo "sarebbe necessario potere assegnare a ciascuna delle cose interdipendenti un indice, è poscia usare della logica matematica, determinando questi indici con un sistema di equazioni".
Egli sostiene che la logica matematica è applicabile solo a fenomeni misurabili, e, allo stato attuale delle nostre conoscenze "ne rimangano esclusi moltissimi tra i quali tutti quelli della sociologia. Poi anche pei fenomeni che si possono misurare, sorgono gravi difficoltà appena il fenomeno è un poco complesso... L' Economia pura giunge sino a porre l'equazione di certi fenomeni, ma non sino a poterle risolvere, almeno in generale. Quindi nelle scienze economiche e sociali, tale metodo... rimane come una meta ideale che nel concreto non si raggiunge quasi mai". Dal "Manuale d'economia politica" e dal "Trattato di sociologia generale". Vilfredo Pareto (1848-1923) ingegnere, economista e sociologo.
Il primo studio di Pareto che qui interessa riportare è relativo alla distribuzione del reddito. La legge di Pareto è una relazione empirica che esprime il numero (N) dei redditieri in funzione del reddito X con a e b parametri positivi da determinare caso per caso. Pareto era pervenuto alla legge analizzando la distribuzione dei redditi di diversi paesi e la riteneva valida a partire da un certo livello minimo di sussistenza. Si tratta di una legge di potenza con esponente negativo che indica che vi sono pochi redditieri con reddito elevato e tanti con reddito basso.

Oggi le leggi di potenza (o scalabili) sono divenute famose dopo i lavori di B. Mandelbrot e la pubblicazione da parte di Nicolas Taleb del libro Il Cigno nero (il Saggiatore, 2009). In pratica si è constatato che in finanza le variazioni dei prezzi dei titoli, dei cambi, delle opzioni, ecc. non seguono una distribuzione normale, ma una legge di potenza con esponente negativo. Le leggi di potenza tendono asintoticamente a zero molto più lentamente di quanto facciano le leggi esponenziali (tra cui la legge normale). Questo fatto implica che variazioni estreme del valore dei titoli, i così detti Cigni Neri, sono molto più frequenti di quanto previsto dalle teorie più accreditate basate sulla campana di Gauss (portafoglio di Markowitz; formula di Merton e Sholes).
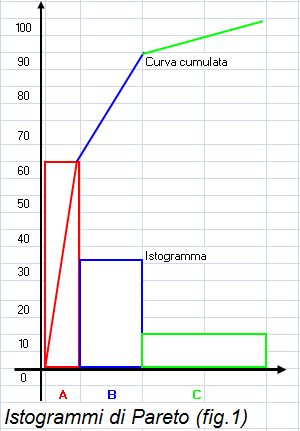
La legge di Pareto diede luogo alla celebre regola empirica dello 80-20 spesso così descritta: il 20% delle persone detiene lo 80% della ricchezza ovvero il 20% dei paesi detiene lo 80% della ricchezza mondiale. Questa regola, nelle organizzazioni aziendali, generò il così detto sistema A,B,C. (figura 1) che ha utilità molteplici: dalle cause di guasto (controllo qualità) al valore del magazzino (controllo scorte) alla classificazione dei rischi (pianificazione dei progetti). In Pratica vi sono i fenomeni di tipo A (pochi, ma vitali), i fenomeni di tipo B (molti ma utili) e i fenomeni di tipo C che, in prima battuta, possono anche essere trascurati.
Il secondo studio si riferisce alla teoria delle scelte che lo portò alla nozione, divenuta celebre di ottimo paretiano (o di soluzioni pareto-ottimali come spesso si dice in teoria dei giochi), il fondamento della moderna economia del benessere: non tanto una situazione in cui l'utilità della società è massima, quanto una situazione in cui non è possibile migliorare la condizione di un individuo senza peggiorare quella di un altro. Analogamente, nei problemi di scelta multicriteri, una soluzione pareto-ottimale è quella in cui non è possibile, cambiando alternativa, migliorare un criterio senza peggiorarne un altro.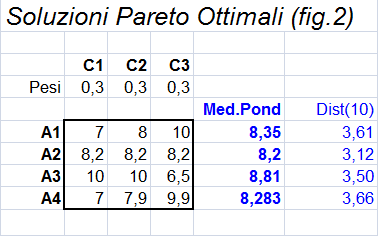

La figura 2 mostra una situazione in cui 4 alternative (A1, A2, A3, A4) debbono essere valutate su 3 criteri (C1, C2, C3) in base ad un punteggio compreso tra 1 e 10 e riportato al centro della tabella. Sotto i criteri sono riportati i rispettivi pesi che nell'esempio sono stati assunti tutti eguali. Le medie ponderate mostrano che la soluzione prescelte è A3 con un punteggio di 8.81 (la peggiore risulta A2 con un punteggio di 8.2). Se invece della media ponderata assumiamo come indice decisionale la minor distanza euclidea dalla situazione ideale (voto 10 su tutti i criteri) la soluzione prescelta è A2 (che ha solo una distanza di 3.12 dalla soluzione ideale). Questo secondo indice privilegia in generale le soluzioni uniformi che non hanno su nessun criterio un punteggio troppo basso (ad esempio il 6.5 che A3 ha sul criterio C3). Le alternative A1, A2, A3 sono tutte pareto ottimali, non lo è invece l'alternativa A4 che risulta dominata dalla alternativa A1 (uguale, ma superiore per almeno un criterio). Pertanto A4 potrebbe essere eliminata a priori.
Le alternative pareto ottimali sono caratterizzate dal fatto che si può sempre trovare un sistema di pesi tale che esse siano preferite (non è così per le alternative dominate).
Purtroppo, nella maggioranza dei problemi decisionali, le alternative pareto ottimali risultano essere molto numerose e tra esse non sempre è facile scegliere la migliore.
Le strategie Pareto Ottimali sono rilevanti anche nella teoria dei giochi (vedi la sezione di matematicamente ad essi dedicata) anche se talora non sono soluzioni di equilibrio come avviene nel dilemma del prigioniero. Forse Pareto non avrebbe condiviso la crescente attenzione che, a partire dal nuovo secolo, ha avuto la neuroeconomia sorta dall'incontro tra discipline diverse: economia, neuroscienze e psicologia cognitiva. Nel 1897 scrisse infatti: "E' empiricamente provato che le scienze naturali sono maggiormente progredite quando si sono basate su principi secondari piuttosto che quando hanno cercato di scoprire l'essenza delle cose... Pertanto l'economia politica ha un grande interesse a basarsi il meno possibile sulla psicologia"