Tangente ad una curva

Si sa che una retta viene identificata da due punti distinti. Tuttavia può essere perfettamente identificata anche da un punto (per il quale passa) e dall'angolo di inclinazione. Per esempio le rette

ed

, che passano per l'origine degli assi cartesiani sono identificate perfettamente, rispettivamente, una volta noti gli angoli

e

.
Questi angoli prendono il nome di "angolo di pendenza" della retta, termine tra l'altro tipico del linguaggio quotidiano. Diciamo infatti che una strada o un pendio hanno una pendenza elevata, quando l'angolo che formano con la linea orizzontale è ampio.

Lo strumento per misurare un angolo è con il goniometro, che ci darà un valore preciso come, per esempio,

.

Di un angolo può spesso essere utile conoscere anche la "tangente". In un triangolo rettangolo

, la tangente di uno dei due angoli acuti si ottiene dividendo la lunghezza del cateto opposto per quello adiacente.

Indicheremo la tangente con il simbolo

o

.

.

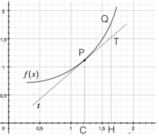
Supponiamo ora di avere una curva continua (questo vuole dire che possiamo tracciarla senza sollevare la matita dal foglio, cioè non presenta discontinuità)

e che si voglia trovare la retta tangente alla stessa, in uno qualsiasi dei suoi punti, che chiameremo

.
Come abbiamo detto prima, una retta è determinata da un punto e da un angolo; visto che il punto lo conosciamo(

), l'unica cosa che dobbiamo fare è trovare il valore della sua pendenza. Senza entrare nel merito di tale ricerca, diremo semplicemente che il matematico Leibniz studiò come determinare tale retta tangente attraverso la costruzione di un particolare triangolo che chiamò triangolo caratteristico, strumento del calcolo infinitesimale.