Consideriamo la seguente funzione:
[math] y = f(x) = \frac{2x^2 - x - 1}{x-1} [/math]
come sappiamo, la funzione è definita per tutti i numeri reali, escluso 1, quindi possiamo scrivere che il suo dominio é:
[math] D \equiv \mathbb{R} - {1} [/math]
Esaminiamo il comportamento della funzione
[math]x=1[/math]
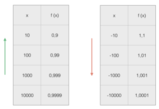
, in cui essa non definita; riassumiamo, quindi, in uno schema i valori che la funzione assume via via che x si avvicina sempre più ad 1:

Possiamo quindi notare che, più si avvicina al valore 1, più f (x) si avvicina al valore 3; in questo caso, si dice che per x che tende a 1, f(x) ha limite 3, oppure che f(x) tende a 3 per x tendente a 1.
Queste affermazioni possono essere riassunte con la seguente scritta:
[math] \displaystyle \lim_{x \rightarrow 1} f(x) = 3[/math]
Ciò significa che la distanza di f(x) dal punto cui tende diminuisce sempre di più all'approssimarsi di x a 1; sappiamo che tale distanza può essere espressa come valore assoluto della differenza tra f(x) e 3, in formula
[math]| f(x) - 3 |[/math]
, infatti abbiamo che:

Possiamo quindi dire che le distanze dei valori di f(x) da 3 possono essere resi piccoli a piacere, cioè possono essere resi più piccoli di qualsiasi numero positivo prefissato, a condizione di scegliere valori di x abbastanza vicini a 1.
In generale, si può verificare che, fissato un numero
[math] \epsilon \gt 0 [/math]
, arbitrariamente piccolo, la distanza di f(x) da 3 risulterà minore di
[math] \epsilon [/math]
per valori di
[math]x \ne 1[/math]
, appartenenti ad un intorno di 1 dipendente da
[math] \epsilon [/math]
.
In questo caso, quindi, dovremmo verificare che la disequazione
[math]| f(x) - 3 | \lt \epsilon[/math]
è soddisfatta per un intorno di x = 1.
[math] |(f(x) - 3| \lt \epsilon \rightarrow \Big|\frac{2x^2-x-1}{x-1}-3\Big| \lt \epsilon \rightarrow \Big|\frac{2x^2-x-1-3x+3}{x-1}\Big| \lt \epsilon[/math]
[math]\Big|\frac{2x^2-4x+2}{x-1}\Big| \lt \epsilon \rightarrow \Big|\frac{2(x-1)^2}{x-1}\Big| \lt \epsilon[/math]
Escludendo il valore x = 1, per il quale la funzione non è definita, possiamo semplificare, e otteniamo:
[math]\Big|\frac{2(x-1)^2}{x-1}\Big| \lt \epsilon \rightarrow |2(x-1)| \lt \epsilon \rightarrow |2x - 2| \lt \epsilon[/math]
[math]-\epsilon \lt 2x - 2 \lt \epsilon \rightarrow 2 - \epsilon \lt 2x \lt \epsilon + 2 \rightarrow 1 - \frac{\epsilon}{2} \lt x \lt \frac{\epsilon}{2} + 1[/math]
Quindi, la disequazione è verificata per appartenente all'intervallo
[math](1 - \epsilon / 2; \epsilon / 2 + 1)[/math]
e
[math]x \ne 1[/math]
, che è un intorno di 1.
Definizione di limite
Diamo ora una definizione generale, considerando una funzione f(x), definita in tutti i punti dell'intervallo [a ; b], escluso al più il punto c, interno all'intervallo.
Si dice che per x tendente a c, la funzione y = f(x) ha per limite l, e si scrive:
[math] \displaystyle \lim_{x \rightarrow c} f(x) = l [/math]
se, comunque si scelga un numero positivo [math] \epsilon [/math]
, arbitrariamente piccolo, si può determinare in corrispondenza di esso, un intorno completo di c tale che per ogni x di tale intorno, escluso al più x = c, si ha che:
[math] |f(x) - l| \lt \epsilon [/math]
che si può anche scrivere come
[math] l - \epsilon \lt f(x) \lt \epsilon + l [/math]
Quindi, per verificare il limite per
[math]x \rightarrow c[/math]
di una funzione f(x), sapendo che tale limite vale l, dobbiamo risolvere la disequazione
[math]| f(x) - l | \lt \epsilon[/math]
: se l'insieme delle soluzioni così determinato è un intorno di c, oppure contiene un intorno completo di c, escluso al più c stesso, il limite verificato.
Esempio di verifica del limite attraverso la definizione
Consideriamo il seguente limite:
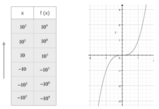
[math] \displaystyle \lim_{x \rightarrow -1} \frac{x^2-2x-3}{x+1} = -4 [/math]
Affinché tale limite sia esatto, dobbiamo imporre che esista un valore
[math] \epsilon [/math]
, piccolo a piacere, tale che la distanza della funzione dal nostro limite, sia minore di
[math] \epsilon [/math]
.
Quindi, impostiamo la seguente disequazione:
[math] \Big|\frac{x^2-2x-3}{x+1} - (-4)\Big| \lt \epsilon [/math]
Risolviamo la disequazione: se il risultato un intorno di -1, il limite sarà verificato:
[math]\Big|\frac{x^2-2x-3}{x+1}+4\Big| \lt \epsilon \rightarrow \Big|\frac{x^2-2x-3+4x+4}{x+1}\Big| \lt \epsilon[/math]
[math]\Big|\frac{x^2+2x+1}{x+1}\Big| \lt \epsilon \rightarrow \Big|\frac{(x+1)^2}{x+1}\Big| \lt \epsilon \rightarrow |x+1| \lt \epsilon[/math]
Da questa espressione otteniamo che:
[math] -\epsilon \lt x+1 \lt \epsilon \rightarrow -1 - \epsilon \lt x \lt \epsilon -1 [/math]
che un intorno di - 1; possiamo quindi concludere affermando che il limite verificato.
Materiale di supporto
Videolezione sui limiti delle funzioni elementari










 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo