Consideriamo la funzione seguente:
Sappiamo che la funzione non definita per x = 1, esaminiamo il comportamento della funzione per valori di x prossimi a 1.
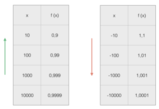
Riassumiamo in una tabella il valore di f(x) per valori di x che si avvicinano sempre di pi a 1, da destra e da sinistra:

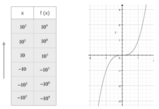
Notiamo, anche facendo riferimento al grafico della funzione, che, a mano a mano che x si approssima per difetto al valore 1, tanto pi la funzione f(x) assume valori negativi pi grandi (in valore assoluto); allo stesso modo, pi x si avvicina a 1 per eccesso, tanto pi i valori positivi di f(x) aumentano.
Possiamo quindi affermare che, per x tendente a 1 da destra, la funzione f(x) tende a
In simboli, scriviamo:
In particolare, possiamo affermare che, all'approssimarsi si x al valore 1, i valori che assume la funzione f(x) diventano maggiori di qualunque numero prefissato, per quanto grande esso possa essere.
Si verifica, quindi, che, comunque scelto un numero M > 0 grande a piacere, si ha sempre che | f(x) | > M, in tutti i punti di x in un intorno di 1, e per
Diamo ora una definizione generale, riferita ad una funzione f(x), definita in un intervallo [a;b], eccetto al pi il punto c, interno all'intervallo.
Definizione:
Si dice che, per x tendente a c, la funzione f(x) ha limite infinito, e si scrive:
se, comunque sia fissato un numero positivo M, arbitrariamente grande, si può determinare in corrispondenza ad esso, un intorno completo di c tale che, per ogni x di tale intorno, escluso al pi x = c, si ha che:
Che si può anche scrivere, ricordando le proprietà del valore assoluto, nel seguente modo:
Ci significa che, nel grafico di f(x), possibile determinare un intorno del punto c tale che, per ogni x appartenente a questo intorno, escluso al pi x = c, i corrispondenti punti del grafico di y = f(x) giacciono all'esterno della striscia delimitata dalle rette y = -M e y = M.
Di conseguenza, per verificare un limite infinito per x che tende ad un valore finito, occorre risolvere la disequazione | f(x) | > M, e accertarsi che l'insieme delle soluzioni sia un intorno di c, o comprenda un intorno di c.
Esempio: Verifichiamo il seguente limite:
Affinchè il limite sia verificato, impostiamo la seguente disequazione:
Dato che al numeratore abbiamo un numero, possiamo separare il valore assoluto, e invertire la frazione:
Possiamo spezzare la disequazione e impostare un sistema, da cui otteniamo:
Risolviamo il sistema, e visualizziamo gli intervalli descritti dalle disequazioni in uno schema:

Poichè il limite di partenza per x che tende a 2, dei due intervalli che costituiscono le soluzioni del sistema, il secondo quello che ci interessa maggiormente.
Infatti, l'intervallo
contiene sicuramente 2, poichè si ha
Quindi, poiché le soluzioni della disequazione contengono un intorno di 2, possiamo concludere che il limite verificato.
Asintoti verticali
Se per
Si può parlare di asintoto verticale destro o sinistro, in base al modo in cui x tende a c: se x tende a c per eccesso, cioè da destra, si avrà un asintoto verticale destro, mentre se x tende a c per difetto, cioè da sinistra, si avrà un asintoto verticale sinistro.
Vediamo un esempio di asintoto verticale facendo riferimento alla funzione dell'esempio precedente:









 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo